第九章:线性映射
一种特殊的函数,因为它简单而又强大。 本章讨论线性映射。映射就是一个函数,输入一个向量,输出另一个向量。线性映射是一类非常有用的特殊函数,既简单又强大。
例 9.1:
图像压缩
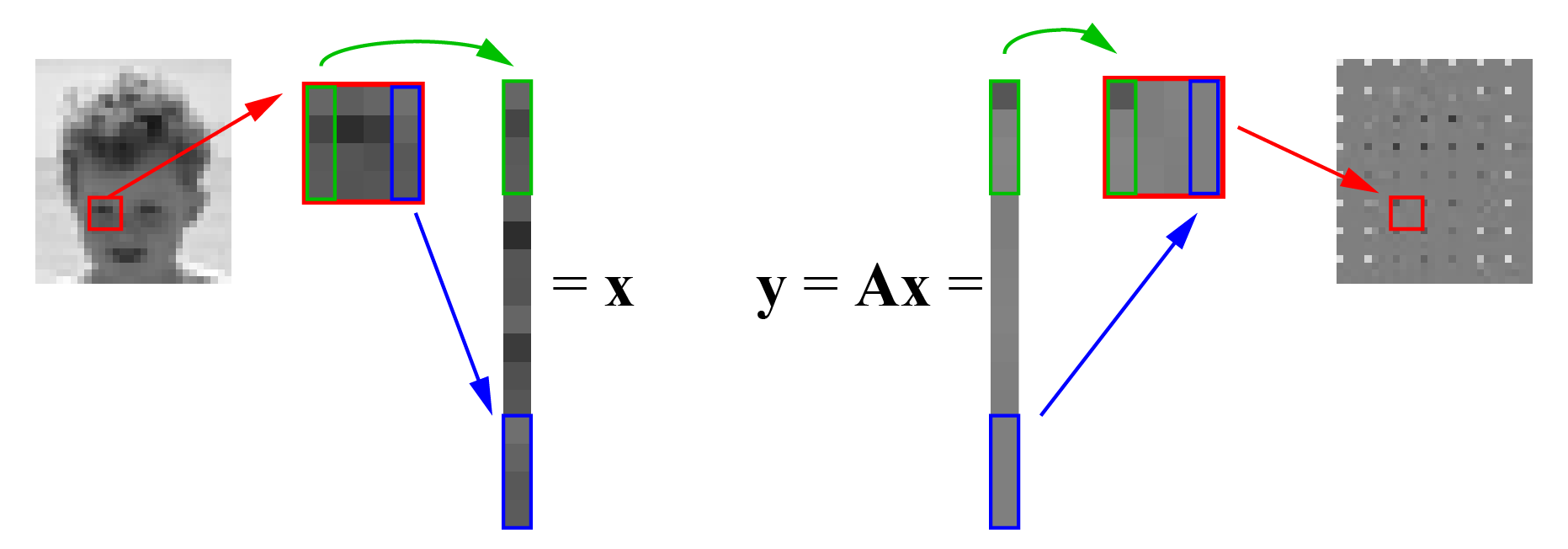
待编码的图像被分成块,例如 $4 \times 4$ 像素块。通常会对每个块直接应用一个线性变换。第一步是将 $4\times 4$ 块按列堆叠成一个 16 维向量 $\vc{x}$,然后用变换矩阵 $\mx{A}$ 乘以该向量,得到新的 16 维向量 $\vc{y}=\mx{A}\vc{x}$,再将其拆分回 $4\times 4$ 图像块。可以看到,变换后的块彼此更加相似:块的第一个值变化较大,但大多数值接近零(图像中为灰色),这意味着这些值可以忽略(设为零)或用更少的比特表示。解码器得到 $\hat{\vc{y}}$,它是 $\vc{y}$ 的近似值,因为部分值可能被设为零或被近似处理。解码器再执行逆变换 $\hat{\vc{x}} = \mx{A}^{-1} \hat{\vc{y}}$,恢复像素亮度的近似值。
线性映射在实际工程问题中非常常见。例如在图像或视频压缩中,待编码的图像会被分成若干块,如图 9.1所示的 $4 \times 4$ 像素块。
与其直接编码每个像素的亮度,不如对每个块进行线性变换。第一步是将 $4\times 4$ 块按列堆叠成一个 16 维向量 $\vc{x}$。然后用变换矩阵 $\mx{A}$ 乘以该向量,得到新的 16 维向量 $\vc{y} =\mx{A}\vc{x}$,再将其拆分回 $4 \times 4$ 图像块。可以看到,变换后的块彼此更加相似。块的第一个值变化较大,但大多数值接近零(图像中为灰色),这意味着这些值可以忽略(设为零)或用更少的比特表示。解码器得到 $\hat{\vc{y}}$,它是 $\vc{y}$ 的近似值,因为部分值可能被设为零或近似处理。解码器再执行逆变换 $\hat{\vc{x}} =\mx{A}^{-1} \hat{\vc{y}}$,恢复像素亮度的近似值。
实际编码器比上述过程更复杂,包含许多优化。例如,线性映射并不直接用矩阵乘法实现,而是用更快但数学上等价的方法。 在 交互式演示 9.2 中,我们展示了一个示例,说明如何在图像上改变可变性。
线性映射在实际工程问题中非常常见。例如在图像或视频压缩中,待编码的图像会被分成若干块,如图 9.1所示的 $4 \times 4$ 像素块。
与其直接编码每个像素的亮度,不如对每个块进行线性变换。第一步是将 $4\times 4$ 块按列堆叠成一个 16 维向量 $\vc{x}$。然后用变换矩阵 $\mx{A}$ 乘以该向量,得到新的 16 维向量 $\vc{y} =\mx{A}\vc{x}$,再将其拆分回 $4 \times 4$ 图像块。可以看到,变换后的块彼此更加相似。块的第一个值变化较大,但大多数值接近零(图像中为灰色),这意味着这些值可以忽略(设为零)或用更少的比特表示。解码器得到 $\hat{\vc{y}}$,它是 $\vc{y}$ 的近似值,因为部分值可能被设为零或近似处理。解码器再执行逆变换 $\hat{\vc{x}} =\mx{A}^{-1} \hat{\vc{y}}$,恢复像素亮度的近似值。
实际编码器比上述过程更复杂,包含许多优化。例如,线性映射并不直接用矩阵乘法实现,而是用更快但数学上等价的方法。 在 交互式演示 9.2 中,我们展示了一个示例,说明如何在图像上改变可变性。
本章首先回顾什么是针对实数(标量)的映射或函数,然后再讨论向量映射。
定义 9.1:
映射
一个映射 $F$ 是一个规则,对于集合 $N$ 中的每一项,都提供集合 $M$ 中的一项
这看起来很抽象,但实际上你已经在处理映射,只不过通常称为函数。另一种表达方式是:
一个映射 $F$ 是一个规则,对于集合 $N$ 中的每一项,都提供集合 $M$ 中的一项
| \begin{equation} F: N \rightarrow M. \end{equation} | (9.1) |
| \begin{equation} y = F(x). \end{equation} | (9.2) |
| \begin{equation} F: x \rightarrow y, x \in N. \end{equation} | (9.3) |
定义 9.1:
映射
一个 映射 $F$ 是一种规则,对于集合 $N$ 中的每个元素, 都在另一个集合 $M$ 中给出一个元素。
竖线符号应读作“使得”或“具有……性质”。在本例中,该表达式可理解为:“$V_F$ 是所有 $x$ 属于集合 $N$ 时 $F(x)$ 的集合”。
对于 $y=x^2$ 这个例子,值域是所有非负实数(包括零),即 $V_F = \mathbb{R}_{\geq 0}$。因此在此情况下,我们只覆盖了陪域的一个子集,即 $V_F$ 是 $M$ 的子集。
一个 映射 $F$ 是一种规则,对于集合 $N$ 中的每个元素, 都在另一个集合 $M$ 中给出一个元素。
| \begin{equation} V_F = \{F(x) | x \in N\}. \end{equation} | (9.4) |
在线性代数中,函数的输入和输出都是向量而不是标量。假设我们有一个坐标系 \(\vc{e}_1,\vc{e}_2\),向量 \(\vc{x}\) 的坐标表示为 \(\begin{pmatrix}x_1 \\\\ x_2 \end{pmatrix}\)。现在可以定义一个函数 \(\vc{y}=F(\vc{x})\),它将每个 \(\vc{x}\) 映射为新的向量 \(\vc{y}=\begin{pmatrix}y_1 \\\\ y_2\end{pmatrix}\),例如:
| \begin{equation} \begin{cases} y_1 = x_1 \\ y_2 = 0 \end{cases} \end{equation} | (9.5) |
一个稍微更有趣的映射例子是以下
| \begin{equation} \begin{cases} y_1 = \cos(\frac{\pi}{3}) x_1 - \sin(\frac{\pi}{3}) x_2, \\ y_2 = \sin(\frac{\pi}{3}) x_1 + \cos(\frac{\pi}{3}) x_2. \end{cases} \end{equation} | (9.6) |
通过操作交互式图示 9.6可以看到,输出向量是输入向量绕原点旋转 $\frac{\pi}{3}$ 后的结果。实际上,我们可以将公式 (9.6)写成矩阵形式:
| \begin{equation} \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \left(\begin{array}{rr} \cos \frac{\pi}{3} & -\sin \frac{\pi}{3} \\ \sin \frac{\pi}{3} & \cos \frac{\pi}{3} \end{array}\right) \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \end{equation} | (9.7) |
| \begin{equation} \vc{y} = \mx{A} \vc{x}. \end{equation} | (9.8) |
交互式图示 9.3中的例子也可以写成矩阵形式:
| \begin{equation} \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \left(\begin{array}{rr} 1 & 0 \\ 0 & 0 \end{array}\right) \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}, \end{equation} | (9.9) |
| \begin{equation} \begin{cases} y_1 = x_1 x_2 + x_2\\ y_2 = x_1 + e^{x_2} \end{cases} \end{equation} | (9.10) |
定义 9.3:
线性映射
线性映射是一个映射 $F$,它满足
第一个条件的直观解释是:无论先求和再应用函数,还是先分别应用函数再求和,得到的结果都是一样的。第二个条件说明按某个因数扩大输入,与扩大输出的效果相同。
线性映射是一个映射 $F$,它满足
| \begin{equation} \begin{cases} F( \vc{x}' + \vc{x}'') = F(\vc{x}') + F(\vc{x}''), \\ F( \lambda \vc{x} ) = \lambda F(\vc{x}). \\ \end{cases} \end{equation} | (9.11) |
例 9.2:
购物车到总价
假设商店只卖通心粉、阿拉比亚塔酱和巧克力。你的购物车内容可以建模为一个向量空间。 两个购物车相加就是把所有商品放到一个车里。标量乘法就是把购物车里的商品数量乘以该标量。注意,实际中购物车乘以非整数或负数并不合理,这使得模型在实际应用时有局限。 引入一组基底购物车:$\vc{e}_1$ 表示含一个通心粉的购物车,$\vc{e}_2$ 表示含一瓶酱的购物车,$\vc{e}_3$ 表示含一块巧克力的购物车。则每个购物车 $\vc{x}$ 可用三个坐标 $(x_1, x_2, x_3)$ 表示:$\vc{x} = x_1 \vc{e}_1 + x_2 \vc{e}_2 + x_3 \vc{e}_3$。
存在一个从购物车 $\vc{x}$ 到价格 $y \in \R$ 的映射。可以引入矩阵 $\vc{A} = \begin{pmatrix}a_{11} & a_{12} & a_{13} \end{pmatrix}$,其中 $a_{11}$ 是通心粉的价格,$a_{12}$ 是酱的价格,$a_{13}$ 是巧克力的价格。总价 $y$ 可表示为 $y = \mx{A} \vc{x}$。
现实中这种映射常常是非线性的,比如“买三送一”等促销。但将映射建模为线性映射通常是合理且有用的。 数学建模与现实总有差异,分析结果需理性和批判性地使用。即使一个通心粉售价为 10,也不代表你能以 10 的价格卖给商店。
假设商店只卖通心粉、阿拉比亚塔酱和巧克力。你的购物车内容可以建模为一个向量空间。 两个购物车相加就是把所有商品放到一个车里。标量乘法就是把购物车里的商品数量乘以该标量。注意,实际中购物车乘以非整数或负数并不合理,这使得模型在实际应用时有局限。 引入一组基底购物车:$\vc{e}_1$ 表示含一个通心粉的购物车,$\vc{e}_2$ 表示含一瓶酱的购物车,$\vc{e}_3$ 表示含一块巧克力的购物车。则每个购物车 $\vc{x}$ 可用三个坐标 $(x_1, x_2, x_3)$ 表示:$\vc{x} = x_1 \vc{e}_1 + x_2 \vc{e}_2 + x_3 \vc{e}_3$。
存在一个从购物车 $\vc{x}$ 到价格 $y \in \R$ 的映射。可以引入矩阵 $\vc{A} = \begin{pmatrix}a_{11} & a_{12} & a_{13} \end{pmatrix}$,其中 $a_{11}$ 是通心粉的价格,$a_{12}$ 是酱的价格,$a_{13}$ 是巧克力的价格。总价 $y$ 可表示为 $y = \mx{A} \vc{x}$。
现实中这种映射常常是非线性的,比如“买三送一”等促销。但将映射建模为线性映射通常是合理且有用的。 数学建模与现实总有差异,分析结果需理性和批判性地使用。即使一个通心粉售价为 10,也不代表你能以 10 的价格卖给商店。
定理 9.1:
线性映射的矩阵形式
映射 $\vc{y} = F(\vc{x})$ 能写成 $\vc{y} = \mx{A}\vc{x}$(矩阵形式)当且仅当它是线性的。
映射 $\vc{y} = F(\vc{x})$ 能写成 $\vc{y} = \mx{A}\vc{x}$(矩阵形式)当且仅当它是线性的。
要证明该定理,需要证明两个方向:每个线性映射都能写成 $\vc{y} = \mx{A}\vc{x}$,以及每个 $\vc{y} = \mx{A}\vc{x}$ 的映射都是线性的。这里以 $\vc{x}$ 和 $\vc{y}$ 都为二维为例,其他维度也类似。
假设 $N$ 和 $M$ 都有一组基底 $\vc{e}_1$、$\vc{e}_2$。则输入 $\vc{x}$ 和输出 $\vc{y}$ 可在该基底下表示为:
| \begin{align} \vc{x} & = x_1 \vc{e}_1 + x_2 \vc{e}_2,\\ \vc{y} & = y_1 \vc{e}_1 + y_2 \vc{e}_2.\\ \end{align} | (9.12) |
| \begin{equation} \vc{y} = F(\vc{x}) = F(x_1 \vc{e}_1 + x_2 \vc{e}_2), \end{equation} | (9.13) |
| \begin{equation} \vc{y} = F(x_1 \vc{e}_1) + F(x_2 \vc{e}_2) = x_1F(\vc{e}_1) + x_2F(\vc{e}_2). \end{equation} | (9.14) |
| \begin{equation} F(\vc{e}_1) = a_{11}\vc{e}_1 + a_{21}\vc{e}_2. \end{equation} | (9.15) |
| \begin{equation} F(\vc{e}_2) = a_{12}\vc{e}_1 + a_{22}\vc{e}_2. \end{equation} | (9.16) |
| \begin{equation} \vc{y} = x_1(a_{11}\vc{e}_1 + a_{21}\vc{e}_2) + x_2(a_{12}\vc{e}_1 + a_{22}\vc{e}_2) = \\ (x_1 a_{11} + x_2 a_{12})\vc{e}_1 + (x_1 a_{21} + x_2 a_{22})\vc{e}_2 \\ \end{equation} | (9.17) |
| (9.18) |
| \begin{equation} \vc{y} = \mx{A}\vc{x}. \end{equation} | (9.19) |
| \begin{equation} F(\vc{x}' + \vc{x}'') = \mx{A}(\vc{x}' + \vc{x}'') = \mx{A}\vc{x}' + \mx{A}\vc{x}'' = F(\vc{x}') + F(\vc{x}''). \end{equation} | (9.20) |
| \begin{equation} F(\lambda \vc{x'}) = \mx{A}(\lambda \vc{x}') = \lambda \mx{A} \vc{x}' = \lambda F(\vc{x'}) \end{equation} | (9.21) |
$\square$
实际应用中,常常需要为某个线性映射找到对应的矩阵 $\mx{A}$。下面的定理会非常有帮助。
定理 9.1:
线性映射的矩阵形式
映射 $\vc{y} = F(\vc{x})$ 能写成 $\vc{y} = \mx{A}\vc{x}$(矩阵形式)当且仅当它是线性的。 在基底 $\vc{e}_1, \vc{e}_2, \ldots, \vc{e}_n$ 下,矩阵 $\mx{A}$ 的列向量就是基底向量的像:$\vc{a}_{,1}=F(\vc{e}_1),\ \vc{a}_{,2}=F(\vc{e}_2),\ \ldots,\ \vc{a}_{,n}=F(\vc{e}_n)$。
映射 $\vc{y} = F(\vc{x})$ 能写成 $\vc{y} = \mx{A}\vc{x}$(矩阵形式)当且仅当它是线性的。 在基底 $\vc{e}_1, \vc{e}_2, \ldots, \vc{e}_n$ 下,矩阵 $\mx{A}$ 的列向量就是基底向量的像:$\vc{a}_{,1}=F(\vc{e}_1),\ \vc{a}_{,2}=F(\vc{e}_2),\ \ldots,\ \vc{a}_{,n}=F(\vc{e}_n)$。
这里以 $N = M = 3$ 为例,其他维度的证明类似。
第一个基底向量 $\vc{e}_1$ 可写为 $\vc{e}_1 = 1 \vc{e}_1 + 0\vc{e}_2 + 0 \vc{e}_3$,坐标为 $(1, 0, 0)$。在公式 $\vc{y} = \mx{A}\vc{x}$ 中取 $\vc{x} = \begin{pmatrix} 1 \\ 0 \\ 0\end{pmatrix}$ 得:
| \begin{equation} \begin{pmatrix} y_1 \\ y_2 \\ y_3\end{pmatrix} = \left(\begin{array}{rrr} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array}\right) \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} = \left(\begin{array}{r} 1 a_{11} + 0 a_{12} + 0 a_{13}\\ 1 a_{21} + 0 a_{22} + 0 a_{23}\\ 1 a_{31} + 0 a_{32} + 0 a_{33}\\ \end{array}\right) = \begin{pmatrix} a_{11} \\ a_{21} \\ a_{31} \end{pmatrix}, \end{equation} | (9.22) |
| \begin{equation} \left(\begin{array}{rrr} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array}\right) \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} = \left(\begin{array}{r} 0 a_{11} + 1 a_{12} + 0 a_{13}\\ 0 a_{21} + 1 a_{22} + 0 a_{23}\\ 0 a_{31} + 1 a_{32} + 0 a_{33}\\ \end{array}\right) = \begin{pmatrix} a_{12} \\ a_{22} \\ a_{32} \end{pmatrix}, \end{equation} | (9.23) |
| \begin{equation} \left(\begin{array}{rrr} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array}\right) \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \left(\begin{array}{r} 0 a_{11} + 0 a_{12} + 1 a_{13}\\ 0 a_{21} + 0 a_{22} + 1 a_{23}\\ 0 a_{31} + 0 a_{32} + 1 a_{33}\\ \end{array}\right) = \begin{pmatrix} a_{13} \\ a_{23} \\ a_{33} \end{pmatrix}, \end{equation} | (9.24) |
$\square$
现在我们可以利用这个结论,通过观察基底向量的像,轻松找到线性映射对应的矩阵 $\mx{A}$。
例 9.3:
求线性映射的矩阵
线性映射 $\vc{y} = F(\vc{x})$ 将二维向量 $\vc{x}$ 逆时针旋转 90 度。当使用标准标准正交基 $\vc{e}_1=(1,0)$、$\vc{e}_2=(0,1)$ 时,求矩阵形式 $\vc{y} = \mx{A} \vc{x}$ 中的变换矩阵 $\mx{A}$。
矩阵 $\mx{A}$ 的第一列是第一个基底向量 $\vc{e}_1$($x$ 轴)的像。将 $x$ 轴逆时针旋转 90 度会平行于 $y$ 轴,坐标为 $(0, 1)$。因此第一列 $\vc{a}_{,1}= \begin{pmatrix} 0 \\ 1 \end{pmatrix}$。
矩阵 $\mx{A}$ 的第二列是第二个基底向量($y$ 轴)的像。将 $y$ 轴逆时针旋转 90 度后得到 $(-1, 0)$。因此第二列 $\vc{a}_{,2} = \begin{pmatrix} -1 \\ 0 \end{pmatrix}$,所以可以写出 $\mx{A}$ as
这如 交互式演示 9.7 所示。
线性映射 $\vc{y} = F(\vc{x})$ 将二维向量 $\vc{x}$ 逆时针旋转 90 度。当使用标准标准正交基 $\vc{e}_1=(1,0)$、$\vc{e}_2=(0,1)$ 时,求矩阵形式 $\vc{y} = \mx{A} \vc{x}$ 中的变换矩阵 $\mx{A}$。
矩阵 $\mx{A}$ 的第一列是第一个基底向量 $\vc{e}_1$($x$ 轴)的像。将 $x$ 轴逆时针旋转 90 度会平行于 $y$ 轴,坐标为 $(0, 1)$。因此第一列 $\vc{a}_{,1}= \begin{pmatrix} 0 \\ 1 \end{pmatrix}$。
矩阵 $\mx{A}$ 的第二列是第二个基底向量($y$ 轴)的像。将 $y$ 轴逆时针旋转 90 度后得到 $(-1, 0)$。因此第二列 $\vc{a}_{,2} = \begin{pmatrix} -1 \\ 0 \end{pmatrix}$,所以可以写出 $\mx{A}$ as
| \begin{equation} \mx{A} = \left(\begin{array}{rr} 0 & -1 \\ 1 & 0 \\ \end{array}\right) . \end{equation} | (9.25) |
$\textcolor{#aa0000}{\vc{e}_1 = \left(\begin{array}{c} 1 \\ 0\\ \end{array}\right)}$
$\textcolor{#0000aa}{\vc{F}(\vc{e}_1) = \left(\begin{array}{c} 0 \\ 1\\ \end{array}\right)}$
$\begin{array}{rr} \textcolor{#0000aa}{0} & \hid{-1} \\ \textcolor{#0000aa}{1} & \hid{0} \\ \end{array}$
$\begin{array}{rr} \textcolor{#0000aa}{0} & \hid{-1} \\ \textcolor{#0000aa}{1} & \hid{0} \\ \end{array}$
$\begin{array}{rr} \hid{0} & \textcolor{#00aa00}{-1} \\ \hid{1} & \textcolor{#00aa00}{0} \\ \end{array}$
$\textcolor{#aa0000}{\vc{e}_2 = \left(\begin{array}{c} 0 \\ 1\\ \end{array}\right)}$
$\textcolor{#00aa00}{\vc{F}(\vc{e}_2) = \left(\begin{array}{r} -1 \\ 0\\ \end{array}\right)}$
$\vc{y} = \left(\begin{array}{rr} \hid{0} & \hid{-1} \\ \hid{1} & \hid{0} \\ \end{array}\right) \vc{x}$
假设我们有一个线性映射 $\vc{y} = F(\vc{x})$,其输出向量 $\vc{y}$ 可以作为另一个线性映射 $\vc{z}= G(\vc{y})$ 的输入。为此,我们需要 $G$ 的定义域等于 $F$ 的陪域。例如,如果 $G(\vc{y})$ 接受二维向量,即 $G$ 的定义域是 $\mathbb{R}^2$,那么 $F$ 的输出也必须是二维向量,即 $F(\vc{x})$ 的陪域也是 $\mathbb{R}^2$。我们称这样的映射
| \begin{equation} \vc{z} = G(F(\vc{x})) \end{equation} | (9.26) |
定理 9.3:
线性映射的复合
如果 $\vc{y} = F(\vc{x})$ 和 $\vc{z} = G(\vc{y})$ 都是线性映射, 则复合映射 $\vc{z} = G(F(\vc{x}))$ 也是线性的。
如果 $\vc{y} = F(\vc{x})$ 和 $\vc{z} = G(\vc{y})$ 都是线性映射, 则复合映射 $\vc{z} = G(F(\vc{x}))$ 也是线性的。
由于 $\vc{y} = F(\vc{x})$ 是线性映射,可以写成矩阵形式 $\vc{y} = \mx{A}\vc{x}$,同样 $\vc{z} = G(\vc{y})$ 也可以写成 $\vc{z} = \mx{B}\vc{y}$。 我们可以写成
| \begin{equation} \vc{z} = \mx{B}\vc{y} = \mx{B}(\mx{A}\vc{x}) = (\mx{B}\mx{A})\vc{x} = \mx{C}\vc{x}, \end{equation} | (9.27) |
$\square$
例 9.4:
线性映射的复合
求一个映射 $F$,它先将二维向量旋转 30 度,然后将 $x$ 坐标乘以二。
我们将其分为两部分。首先求一个映射 $\vc{y} =G(\vc{x})$ 旋转 30 度,然后求另一个映射 $\vc{z} = H(\vc{y})$ 将 $x$ 坐标乘以二。
设 $\mx{A}$ 为 $G$ 的变换矩阵。由定义 6.10 可知,旋转角度 $\phi$ 由 $ \left(\begin{array}{rr} \cos \phi & -\sin \phi \\ \sin \phi & \cos \phi \end{array}\right)$ 得到。 因此,设 $\phi = \frac{\pi}{6}$,得
令 $\mx{B}$ 为映射 $H$ 的变换矩阵。其任务是将 $x$ 坐标乘以二,同时保持 $y$ 坐标不变。对此我们可以设置如下矩阵:
最后,复合映射 $\vc{z} = H(G(\vc{x}))$ 的变换矩阵 $\mx{C}$ 为:
求一个映射 $F$,它先将二维向量旋转 30 度,然后将 $x$ 坐标乘以二。
我们将其分为两部分。首先求一个映射 $\vc{y} =G(\vc{x})$ 旋转 30 度,然后求另一个映射 $\vc{z} = H(\vc{y})$ 将 $x$ 坐标乘以二。
设 $\mx{A}$ 为 $G$ 的变换矩阵。由定义 6.10 可知,旋转角度 $\phi$ 由 $ \left(\begin{array}{rr} \cos \phi & -\sin \phi \\ \sin \phi & \cos \phi \end{array}\right)$ 得到。 因此,设 $\phi = \frac{\pi}{6}$,得
| \begin{equation} \mx{A} = \left(\begin{array}{rr} \frac{\sqrt{3}}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{\sqrt{3}}{2} \end{array}\right). \end{equation} | (9.28) |
| \begin{equation} \mx{B} = \left(\begin{array}{rr} 2 & 0 \\ 0 & 1 \end{array}\right). \end{equation} | (9.29) |
| \begin{equation} \mx{C} = \mx{B}\mx{A} =\left(\begin{array}{rr} 2 & 0 \\ 0 & 1 \end{array}\right) \left(\begin{array}{rr} \frac{\sqrt{3}}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{\sqrt{3}}{2} \end{array}\right) = \left(\begin{array}{rr} \sqrt{3} & -1 \\ \frac{1}{2} & \frac{\sqrt{3}}{2} \end{array}\right). \end{equation} | (9.30) |
对于某些映射,多个输入 $\vc{x}$ 可能映射到相同的值 $F(\vc{x})$。例如在交互式图示 9.5中,我们只是将点投影到 $x$ 轴上(通过将 $y$ 坐标设为零),那么 $\vc{x}_1 = (1,5)$ 和 $\vc{x}_2 = (1,2)$ 都会映射到同一点 $(1,0) = F(\vc{x}_1) =F(\vc{x}_2)$。但对于某些映射,结果是唯一的,即如果 $\vc{x}_1 \neq \vc{x}_2$,则 $F(\vc{x}_1) \neq F(\vc{x}_2)$。我们称这样的映射为单射。
定义 9.4:
单射映射
映射 $y = F(x)$ 是单射,如果任意两个不同的向量 $\vc{x}_1 \neq \vc{x}_2$ 总是给出两个不同的像 $F(\vc{x}_1) \neq F(\vc{x}_2)$。
另一种等价的表述是:一个单射映射具有这样的性质:如果两个像 $F(\vc{x}_1)$ 和 $F(\vc{x}_2)$ 相等,则 $\vc{x}_1$ 必须等于 $\vc{x}_2$。
映射 $y = F(x)$ 是单射,如果任意两个不同的向量 $\vc{x}_1 \neq \vc{x}_2$ 总是给出两个不同的像 $F(\vc{x}_1) \neq F(\vc{x}_2)$。
对于某些映射 $\vc{y} = F(\vc{x})$,我们可以通过选择合适的 $\vc{x}$ 到达陪域中的每一点 $\vc{y}$。当映射的值域覆盖陪域时,我们称这样的映射为满射。既是单射又是满射的映射称为双射。
定义 9.5:
满射映射
映射 $\vc{y} =F(\vc{x})$,其中 $\vc{x} \in N$ 和 $\vc{y} \in M$ 是满射,如果值域 $V_F$ 等于陪域 $M$, 即 $V_F = M$。
映射 $\vc{y} =F(\vc{x})$,其中 $\vc{x} \in N$ 和 $\vc{y} \in M$ 是满射,如果值域 $V_F$ 等于陪域 $M$, 即 $V_F = M$。
定义 9.6:
双射映射
一个映射是双射,当且仅当它既是单射又是满射。
我们现在将通过几个映射的例子,来研究它们是否是单射、满射以及双射。
一个映射是双射,当且仅当它既是单射又是满射。
例 9.5:
映射类型 I
考虑映射 $\vc{y} = F(\vc{x})$
其中 $\vc{x}$ 属于定义域 $N = \mathbb{R}^2$,
结果向量 $\vc{y}$ 属于陪域 $M =\mathbb{R}^2$。这个映射是单射,因为如果我们有两个不同的输入值 $\vc{a}$ 和 $\vc{b}$,输出向量 $\begin{pmatrix}e^{a_1}\\e^{a_2}\end{pmatrix}$ 将不同于 $\begin{pmatrix}e^{b_1}\\e^{b_2}\end{pmatrix}$,除非 $\vc{a} =\vc{b}$。然而,该映射不是满射,因为不可能得到 $y_1$ 和 $y_2$ 的负值(对于所有实数 $x$ 都有 $e^x > 0$)。值域 $V_F$ 在这种情况下仅为象限 $y_1 > 0, y_2 > 0$,不等于陪域 $M =\mathbb{R}^2$。由于该映射不是满射,所以它也不是双射。
考虑映射 $\vc{y} = F(\vc{x})$
| \begin{equation} \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = F\left(\begin{pmatrix} x_1 \\ x_2 \end{pmatrix}\right) = \left(\begin{array}{r} e^{x_1} \\ e^{x_2} \end{array}\right) , \end{equation} | (9.31) |
例 9.6:
映射类型 II
研究映射 $\vc{y} = F(\vc{x})$
是双射。在这种情况下,定义域 $N$ 和陪域 $M$ 都等于实数平面 $\mathbb{R}^2$。
首先我们研究它是否是单射。很明显它是,因为两个不同的输入值 $\vc{a}$ 和 $\vc{b}$ 会产生两个不同的输出向量 $\begin{pmatrix}2 a_1\\3a_2\end{pmatrix} \neq \begin{pmatrix}2b_1\\3b_2\end{pmatrix}$,除非 $\vc{a} = \vc{b}$。
同时所有输出向量 $\begin{pmatrix}y_1\\y_2\end{pmatrix}$(整个陪域 $M = \mathbb{R}^2$)都可以通过使用 输入 $\begin{pmatrix}x_1\\ x_2\end{pmatrix}= \begin{pmatrix}\frac{y_1}{2}\\\frac{y_2}{3}\end{pmatrix}$ 到达。这 意味着映射也是满射。由于映射 既是单射又是满射,所以它是双射。
事实证明,线性映射中是双射的具有许多有用的性质。例如,找到逆映射很简单,如我们将在以下定理中看到的。
研究映射 $\vc{y} = F(\vc{x})$
| \begin{equation} \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = F\left(\begin{pmatrix} x_1 \\ x_2 \end{pmatrix}\right) = \left(\begin{array}{r} 2 x_1 \\ 3 x_2 \end{array}\right) \end{equation} | (9.32) |
首先我们研究它是否是单射。很明显它是,因为两个不同的输入值 $\vc{a}$ 和 $\vc{b}$ 会产生两个不同的输出向量 $\begin{pmatrix}2 a_1\\3a_2\end{pmatrix} \neq \begin{pmatrix}2b_1\\3b_2\end{pmatrix}$,除非 $\vc{a} = \vc{b}$。
同时所有输出向量 $\begin{pmatrix}y_1\\y_2\end{pmatrix}$(整个陪域 $M = \mathbb{R}^2$)都可以通过使用 输入 $\begin{pmatrix}x_1\\ x_2\end{pmatrix}= \begin{pmatrix}\frac{y_1}{2}\\\frac{y_2}{3}\end{pmatrix}$ 到达。这 意味着映射也是满射。由于映射 既是单射又是满射,所以它是双射。
定理 9.4:
逆映射的等价性
对于从 $\vc{x} \in \mathbb{R}^n$ 到 $\vc{y} \in \mathbb{R}^n$ 的线性映射 $\vc{y} = F(\vc{x})$,以下三个陈述是等价的:
对于从 $\vc{x} \in \mathbb{R}^n$ 到 $\vc{y} \in \mathbb{R}^n$ 的线性映射 $\vc{y} = F(\vc{x})$,以下三个陈述是等价的:
- 映射 $F$ 是双射。
- $F$ 的变换矩阵是可逆的。
- 基向量 $\vc{e}_1, \, \ldots, \, \vc{e}_n$ 的映像 $F(\vc{e}_1), \ldots, F(\vc{e}_n)$ 在 $\mathbb{R}^n$ 中构成一个基。
i $\rightarrow$ ii: 如果映射 $F$ 是双射,这意味着方程 $F(\vc{x}) = \vc{y}$ 对于每个 $\vc{y}$ 都有唯一解 $\vc{x}$。特别是,由于 $F$ 是单射,我们知道如果 $F(\vc{u})=F(\vc{v})$,则 $\vc{u}$ 必须等于 $\vc{v}$。另外,由于 $F$ 是满射,每个 $\vc{y}$ 都可以通过适当的 $\vc{x}$ 到达。$F$ 的矩阵形式为 $\vc{y} = \mx{A}\vc{x}$,该方程对每个 $\vc{y}$ 都有唯一解等价于说 $\mx{A}$ 根据 定理 6.9是可逆的。
ii $\rightarrow$ iii: 根据 定理 9.2,$F(\vc{e}_1)$ 恰好是 $\mx{A}$ 的第一列。同样,$F(\vc{e}_2)$ 是第二列,依此类推。定理 6.9 告诉我们,如果 $\mx{A}$ 是可逆的,则 $\mx{A}$ 的列跨越 $\mathbb{R}^n$,这意味着它们在 $\mathbb{R}^n$ 中形成一个基。
iii $\rightarrow$ i: 我们首先证明 iii 意味着 $F$ 是单射,即如果 $F(\vc{u}) = F(\vc{v})$ 则 $\vc{u}$ 必须等于 $\vc{v}$。
我们可以写 $\vc{u} = u_1 \vc{e}_1 + u_2 \vc{e}_2 + \ldots + u_n\vc{e}_n$ 和 $\vc{v} = v_1 \vc{e}_1 + v_2 \vc{e}_2 + \ldots + v_n\vc{e}_n$。我们知道 $F(\vc{u}) = F(\vc{v})$,因此 $F(\vc{u})-F(\vc{v}) = \vc{0}$,这等价于
| \begin{equation} F(u_1 \vc{e}_1 + u_2 \vc{e}_2 + \ldots + u_n\vc{e}_n) - F(v_1 \vc{e}_1 + v_2 \vc{e}_2 + \ldots + v_n\vc{e}_n) = \vc{0}. \end{equation} | (9.33) |
| \begin{equation} u_1 F(\vc{e}_1) + u_2 F(\vc{e}_2) + \ldots + u_nF(\vc{e}_n) - \Big( v_1 F(\vc{e}_1) + v_2 F(\vc{e}_2) + \ldots + v_nF(\vc{e}_n)\Big) = \vc{0}. \end{equation} | (9.34) |
| \begin{equation} (u_1-v_1) F(\vc{e}_1) + (u_2 - v_2) F(\vc{e}_2) + \ldots + (u_n - v_n) F(\vc{e}_n) = \vc{0}, \end{equation} | (9.35) |
然后我们证明 $\vc{y} = F(\vc{x})$ 是满射,即我们可以通过适当选择 $\vc{x}$ 来达到每个 $\vc{y}$。
我们可以写 $\vc{x} = x_1\vc{e}_1 + x_2\vc{e}_2 + \ldots + x_n\vc{e}_n$,因此 $\vc{y} = F(\vc{x})$ 可以写为
| \begin{equation} \vc{y} = F(\vc{x}) = F(x_1\vc{e}_1 + x_2\vc{e}_2 + \ldots + x_n\vc{e}_n)。 \end{equation} | (9.36) |
| \begin{equation} \vc{y} = x_1F(\vc{e}_1) + x_2F(\vc{e}_2) + \ldots x_n F(\vc{e}_n), \end{equation} | (9.37) |
$\square$
从这个证明中,以下定理是随之而来的。
定理 9.5:
逆映射矩阵
对于具有变换矩阵 $\mx{A}$ 的双射线性映射 $\vc{y} = F(\vc{x})$,逆映射 $\vc{x} =F^{-1}(\vc{y})$ 是线性的,其变换矩阵为 $\inv{\mx{A}}$。
对于具有变换矩阵 $\mx{A}$ 的双射线性映射 $\vc{y} = F(\vc{x})$,逆映射 $\vc{x} =F^{-1}(\vc{y})$ 是线性的,其变换矩阵为 $\inv{\mx{A}}$。
我们要寻找一个映射 $\inv{F}$,使得 $\inv{F}(F(\vc{x})) = \vc{x}$。
考虑矩阵形式的 $\vc{y} = F(\vc{x})$
| \begin{equation} \vc{y} = \mx{A}\vc{x}。 \end{equation} | (9.38) |
| \begin{equation} \inv{\mx{A}}\vc{y} = \inv{\mx{A}}\mx{A}\vc{x} = \mx{I} \vc{x} = \vc{x}, \end{equation} | (9.39) |
| \begin{equation} \vc{x} = \inv{\mx{A}} \vc{y}。 \end{equation} | (9.40) |
$\square$
在 交互式演示 9.8 中,我们展示了如何使用线性映射来生成阴影效果。
例 9.7:
阴影
假设我们有一个通过原点的平面,其法向量为 $\vc{n} = (0, 1, 0)$。此外,假设太阳距离原点无限远,位于方向 $\vc{r} = (0.5,1.0, 0.25)$ 上。我们在平面上方有很多点,想知道它们在平面上的阴影。还假设我们已被告知这种特殊类型的阴影投影可以表示为线性映射。
逐点计算阴影点是可能的,但如果我们能创建一个线性映射 $\vc{y} =\mx{A}\vc{x}$,以便我们可以直接通过简单地将点 $\vc{x}$ 与矩阵 $\mx{A}$ 相乘来获取投影点 $\vc{y}$,这会更方便。鉴于问题是线性的,这应该是可能的。
在这种情况下,我们利用 定理 9.2,即为了获得 $\mx{A}$,我们只需要知道三个单位向量发生了什么。变换矩阵 $\mx{A}$ 的第一列向量就是第一个单位向量 $\vc{e_1} = (1,0,0)$ 的映像,以此类推。因此,如果我们找出点 $(1,0,0)$ 的阴影在平面上落在哪里,我们就有了 $\mx{A}$ 的第一列。
我们可以将平面写成 $ax+by+cz+d = 0$ 的形式,由于我们知道法向是 $(0, 1, 0)$,这简化为 $y+d=0$。此外,由于原点 $(0, 0, 0)$ 在平面上,方程进一步简化为 $y=0$。我们现在可以取通过点 $(p_x, p_y, p_z)$ 的直线并沿太阳方向 $(r_x, r_y, r_z)$ 跟随它,
将此直线方程代入平面方程应该给我们距离 $\lambda$,我们需要从 $P$ 的旅程以达到交点。当我们将其插入平面方程 $y = 0$ 时,我们得到 $p_y + 1.0 \lambda = 0$。对于第一个单位向量 $\vc{e}_1=(1, 0, 0)$,我们有 $p_y = 0$,得到 $0 + \lambda = 0$,这意味着 $\lambda = 0$。交点因此在 $(1, 0, 0) + 0\vc{r} = (1, 0, 0)$。这因此是 $\mx{A}$ 的第一列。对于第二个单位向量 $\vc{e}_2 = (0, 1, 0)$,我们有 $p_y = 1$,给出方程 $1+\lambda = 0$,或 $\lambda = -1$。因此 $\mx{A}$ 的第二列是 $(0, 1, 0) + (-1)(0.5, 1.0, 0.25) = (-0.5, 0, -0.25)$。第三个单位向量 $\vc{e}_3 = (0, 0, 1)$ 得到 $\lambda = 0$,因此 $\mx{A}$ 的最后一列是 $(0, 0, 1) - 0\vc{r} = (0, 0, 1)$。
总结一下,我们现在创建了一个线性映射 $\vc{y} = \mx{A}\vc{x}$,它取一个点 $\vc{x}$ 并将其映射到其阴影 $\vc{y}$。矩阵 $\mx{A}$ 等于
这用于下图中。立方体的每个点只是使用上面的矩阵 $\mx{A}$ 的 $\vc{y} = \mx{A}\vc{x}$ 投影到平面上。通过使用投影坐标而不是原始坐标绘制立方体的每个面,可以绘制立方体的阴影。
现在我们有了这个阴影示例,我们可以研究映射是否是双射。
假设我们有一个通过原点的平面,其法向量为 $\vc{n} = (0, 1, 0)$。此外,假设太阳距离原点无限远,位于方向 $\vc{r} = (0.5,1.0, 0.25)$ 上。我们在平面上方有很多点,想知道它们在平面上的阴影。还假设我们已被告知这种特殊类型的阴影投影可以表示为线性映射。
逐点计算阴影点是可能的,但如果我们能创建一个线性映射 $\vc{y} =\mx{A}\vc{x}$,以便我们可以直接通过简单地将点 $\vc{x}$ 与矩阵 $\mx{A}$ 相乘来获取投影点 $\vc{y}$,这会更方便。鉴于问题是线性的,这应该是可能的。
在这种情况下,我们利用 定理 9.2,即为了获得 $\mx{A}$,我们只需要知道三个单位向量发生了什么。变换矩阵 $\mx{A}$ 的第一列向量就是第一个单位向量 $\vc{e_1} = (1,0,0)$ 的映像,以此类推。因此,如果我们找出点 $(1,0,0)$ 的阴影在平面上落在哪里,我们就有了 $\mx{A}$ 的第一列。
我们可以将平面写成 $ax+by+cz+d = 0$ 的形式,由于我们知道法向是 $(0, 1, 0)$,这简化为 $y+d=0$。此外,由于原点 $(0, 0, 0)$ 在平面上,方程进一步简化为 $y=0$。我们现在可以取通过点 $(p_x, p_y, p_z)$ 的直线并沿太阳方向 $(r_x, r_y, r_z)$ 跟随它,
| \begin{equation} \begin{pmatrix} x \\ y \\ z \end{pmatrix}= \begin{pmatrix} p_x \\ p_y \\ p_z \end{pmatrix}+ \lambda \begin{pmatrix} r_x \\ r_y \\ r_z \end{pmatrix} = \begin{pmatrix} p_x \\ p_y \\ p_z \end{pmatrix}+ \lambda \begin{pmatrix} 0.5 \\ 1.0 \\ 0.25 \end{pmatrix}. \end{equation} | (9.41) |
总结一下,我们现在创建了一个线性映射 $\vc{y} = \mx{A}\vc{x}$,它取一个点 $\vc{x}$ 并将其映射到其阴影 $\vc{y}$。矩阵 $\mx{A}$ 等于
| \begin{equation} \mx{A} = \left(\begin{array}{ccc} 1 & -0.5 & 0\\ 0 & 0 & 0\\ 0 & -0.25 & 1\\ \end{array}\right). \end{equation} | (9.42) |
例 9.8:
阴影的双射性
检查 例 9.7 中的映射是否是双射。
根据 定理 9.4,当且仅当变换矩阵 $\mx{A}$ 可逆时,映射 $\vc{y} = \mx{A}\vc{x}$ 是双射。我们从关于行列式的 定理 7.10 知道矩阵仅当行列式非零时才是可逆的。然而,行列式
必定为零,因为第二行为零(参见 定理 7.1$(iv)$ 结合 $(vii)$)。因此该映射不能是双射。
这是有道理的。如果你知道一组点和太阳的方向,你可以计算他们各自的阴影。然而,如果你只有阴影和太阳的方向,你无法恢复原始位置,因为你只知道该点位于的方向,而不知道它的距离。因此该操作不可逆,或用正式术语,双射。
检查 例 9.7 中的映射是否是双射。
根据 定理 9.4,当且仅当变换矩阵 $\mx{A}$ 可逆时,映射 $\vc{y} = \mx{A}\vc{x}$ 是双射。我们从关于行列式的 定理 7.10 知道矩阵仅当行列式非零时才是可逆的。然而,行列式
| \begin{equation} \det(\mx{A}) = \left|\begin{array}{ccc} 1 & -0.5 & 0\\ 0 & 0 & 0\\ 0 & -0.25 & 1\\ \end{array}\right| \end{equation} | (9.43) |
这是有道理的。如果你知道一组点和太阳的方向,你可以计算他们各自的阴影。然而,如果你只有阴影和太阳的方向,你无法恢复原始位置,因为你只知道该点位于的方向,而不知道它的距离。因此该操作不可逆,或用正式术语,双射。
例 9.9:
重新审视图像压缩
在 例 9.1 中,我们看到映射 $\vc{y} = \mx{A}\vc{x}$ 被用作压缩过程的一部分。这个映射可能是双射吗?
答案是肯定的。为了有用,我们希望解码后的图像与原始图像看起来相同,至少在我们花费足够的比特时是这样。如果我们有一个不是双射的映射,信息将在变换步骤 $\vc{y} = \mx{A}\vc{x}$ 中丢失。无论我们如何保存 $\vc{y}$,即无论我们花多少比特来描述 $\vc{y}$,都不可能恢复 $\vc{x}$。如果另一方面映射是双射,使用 $\vc{x} = \inv{\mx{A}}\vc{y}$ 恢复 $\vc{x}$ 很简单。
在 例 9.1 中,我们看到映射 $\vc{y} = \mx{A}\vc{x}$ 被用作压缩过程的一部分。这个映射可能是双射吗?
答案是肯定的。为了有用,我们希望解码后的图像与原始图像看起来相同,至少在我们花费足够的比特时是这样。如果我们有一个不是双射的映射,信息将在变换步骤 $\vc{y} = \mx{A}\vc{x}$ 中丢失。无论我们如何保存 $\vc{y}$,即无论我们花多少比特来描述 $\vc{y}$,都不可能恢复 $\vc{x}$。如果另一方面映射是双射,使用 $\vc{x} = \inv{\mx{A}}\vc{y}$ 恢复 $\vc{x}$ 很简单。