定理 7.10:
对任意方阵 $\mx{A}$,如下命题等价:
\begin{equation}
\begin{array}{ll}
(i) & \spc\text{$\mx{A}$ 的列向量构成一组基} \\
(ii) & \spc\text{$\mx{A}$ 的行向量构成一组基} \\
(iii) & \spc\text{矩阵方程}\spc \mx{A} \vc{x} = 0 \spc\text{仅有零解}\spc \vc{x}=0 \\
(iv) & \spc\text{矩阵方程}\spc \mx{A} \vc{x} = \vc{y} \spc\text{对任意}\spc \vc{y} \spc\text{都有解} \\
(v) & \spc\text{$\mx{A}$ 可逆} \\
(vi) & \spc\det \mx{A} \neq 0 \\
\end{array}
\end{equation}
定理 10.3:
矩阵 $\mx{A}$ 可对角化当且仅当存在由特征向量构成的基。并且在分解
$ \mx{A} = \mx{V} \mx{D} \mx{V}^{-1}$ 中,$\mx{V}$ 的列对应特征向量,$\mx{D}$ 的对角元对应特征值。
定理 10.4:
若 $n \times n$ 矩阵 $\mx{A}$ 拥有 $n$ 个彼此不同的特征值,则 $\mx{A}$ 可对角化。此外,属于不同特征值的 $n$ 个特征向量总是线性无关的。
定理 10.8:
对称矩阵 $\mx{A}$ 存在正交矩阵 $\mx{U}$ 与对角矩阵 $\mx{D}$,使得
\begin{equation}
\mx{A} = \mx{U} \mx{D} \mx{U}^{-1} = \mx{U} \mx{D} \mx{U}^{T} .
\end{equation}
换言之,可以使用由特征向量构成的规范正交基来进行对角化。
定理 10.7:
对称矩阵 $\mx{A}$ 的所有特征值均为实数。
定理 10.9:正定性与特征值
实对称的 $n \times n$ 矩阵 $\mx{A}$满足:
\begin{align}
\begin{array}{ll}
&(1) & \text{当且仅当所有特征值均为正时,正定} \\
&(2) & \text{当且仅当所有特征值均为非负时,半正定} \\
&(3) & \text{当且仅当所有特征值均为负时,负定} \\
&(4) & \text{当且仅当所有特征值均为非正时,半负定} \\
&(5) & \text{当存在正、负特征值时,不定} \\
\end{array}
\end{align}
公式 10.68:
\begin{equation}
s^2 = \frac{\vc{w}^\T \mx{D} \vc{w}}{\vc{w}^\T \vc{w}}.
\end{equation}
定理 8.8:维数定理
对于 $m\times n$ 矩阵 $\mx{A}$(即有 $n$ 列),有
\begin{equation}
\rank(\mx{A}) + \nullity(\mx{A}) = n.
\end{equation}
定理 8.9:
矩阵 $\mx{A}$(大小为 $m\times n$)的秩是使得某个 $r\times r$ 余子式不为零的最大整数 $r$。
定义 10.4:
若存在可逆矩阵 $\mx{V}$ 与对角矩阵 $\mx{D}$ 满足下式,则称矩阵 $\mx{A}$ 可对角化:
\begin{equation}
\mx{A} = \mx{V} \mx{D} \mx{V}^{-1} .
\end{equation}
定理 7.1:行列式的性质
\begin{equation}
\begin{array}{llr}
(iv) & \begin{vmatrix} \ldots & \vc{0} & \ldots \end{vmatrix}
= 0 & \spc\text{(若某列为零,则行列式为零)} \\
(v) & \begin{vmatrix} \ldots & \vc{a}_i & \ldots & \vc{a}_j & \ldots \end{vmatrix}
= -
\begin{vmatrix} \ldots & \vc{a}_j & \ldots & \vc{a}_i & \ldots \end{vmatrix}
& \spc\text{(交换两列)} \\
(vi) & \begin{vmatrix} \ldots & \vc{a}_i & \ldots & \vc{a}_j & \ldots \end{vmatrix}
=
\begin{vmatrix} \ldots & \vc{a}_i+\lambda \vc{a}_j & \ldots & \vc{a}_j & \ldots \end{vmatrix}
& \spc\text{(某列加上另一列的倍数)} \\
(vii) & \det( \mx{A}) = \det( \mx{A}^\T) & \spc\text{(转置)} \\
(viii) & \det( \mx{A} \mx{B}) = \det( \mx{A}) \det( \mx{B}) & \spc\text{(乘积)} \\
(ix) & \det( \mx{A}^{-1}) = \frac{1}{\det( \mx{A})} & \spc\text{(逆)} \\
\end{array}
\end{equation}
公式 10.125:
\begin{equation}
\begin{cases}
\begin{array}{rrrl}
x_1(t) = a_1 r_{11} \sin( \sqrt{-\lambda_1} t + \phi_1) + a_2 r_{12} \sin( \sqrt{-\lambda_2} t + \phi_2) + a_3 r_{13} \sin( \sqrt{-\lambda_3} t + \phi_3), \\
x_2(t) = a_1 r_{21} \sin( \sqrt{-\lambda_1} t + \phi_1) + a_2 r_{22} \sin( \sqrt{-\lambda_2} t + \phi_2) + a_3 r_{23} \sin( \sqrt{-\lambda_3} t + \phi_3), \\
x_3(t) = a_1 r_{31} \sin( \sqrt{-\lambda_1} t + \phi_1) + a_2 r_{32} \sin( \sqrt{-\lambda_2} t + \phi_2) + a_3 r_{33} \sin( \sqrt{-\lambda_3} t + \phi_3). \\
\end{array}
\end{cases}
\end{equation}
公式 10.124:
\begin{equation}
\begin{cases}
\begin{array}{rrrl}
z_1(t) = a_1 \sin( \sqrt{-\lambda_1} t + \phi_1), \\
z_2(t) = a_2 \sin( \sqrt{-\lambda_2} t + \phi_2), \\
z_3(t) = a_3 \sin( \sqrt{-\lambda_3} t + \phi_3).
\end{array}
\end{cases}
\end{equation}
公式 10.127:
\begin{equation}
\begin{cases}
\begin{array}{rrrl}
\dot{z}_1(t) = a_1 \sqrt{-\lambda_1}\cos( \sqrt{-\lambda_1} t + \phi_1), \\
\dot{z}_2(t) = a_2 \sqrt{-\lambda_1}\cos( \sqrt{-\lambda_2} t + \phi_2), \\
\dot{z}_3(t) = a_3 \sqrt{-\lambda_1}\cos( \sqrt{-\lambda_3} t + \phi_3).
\end{array}
\end{cases}
\end{equation}
第10章:特征值与特征向量
在本章中,我们介绍方阵的与的概念。它们具有广泛应用,例如更好地理解与可视化、分析机械结构的稳定性、求解微分方程组、进行图像识别、解释与可视化二次方程,以及用于图像分割。我们先从两个例子开始。
例 10.1:
特征脸
识别图像中的人脸的方法很多。当前最先进的方法通常采用深度学习,而代数是其中的重要组成部分。一种理解和压缩人脸图像的常用方法是所谓的“特征脸”。这在
交互插图 10.1中有所展示:我们示例说明如何用两个参数生成新的面孔。只需指定两个数字,就可以合成如图所示的一整组图像。因此,该技术可用于
图像合成;也可视为
图像压缩,因为每幅新图像只需存储两个数。该技术还可用于
图像理解:对新的图像,可以计算其对应的坐标 $(x_1,x_2)$。在 $R^2$ 的不同区域对应微笑、张口等不同表情。
平均图像 $\vc{O}$ 以及两个特征脸 $\vc{E}_1$ 与 $\vc{E}_2$ 如下所示。
用于生成 $\vc{O}$、$\vc{E}_1$ 和 $\vc{E}_2$ 的图像见
图 10.2。在学习更多与之后,我们会在
例 10.18对该过程做更详细解释。简要来说,
图 10.2中的图像用于计算均值 $O$ 和协方差矩阵。协方差矩阵对应最大两个特征值的被用作 $\vc{E}_1$ 与 $\vc{E}_2$。
例 10.2:
PageRank
谷歌如何给网页排序?
在本例中,我们考察一个用于网页排序的简化模型。核心思想是:如果许多网页(且这些网页本身排序较高)链接到某个网页,那么该网页的排序就更高。该问题具有递归性:为了计算某一网页的排序,需要知道其他网页的排序。另一种视角是将用户视为随机点击主页上其中一个链接的人。经过随机浏览后,页面就是你处在某个主页上的概率。为连接所有主页,常见做法是以一个较小的概率(例如 15%)跳转到任意主页。我们来看一个玩具示例。
假设互联网上只有四个主页,1 - 'Immersive Math',2 - '代数',3 - '布尔代数',4 - '无聊代数'。
从一个主页到另一个主页的链接在图中用箭头表示。
设处在各主页上的概率由向量 $\vc{v} = \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \end{pmatrix}$ 给出,其中 $v_i$ 是处在编号为 $i$ 的主页上的概率。如果在某个主页上随机选择其链接,则处在各主页上的概率变为 $ \vc{w} = \mx{A} \vc{v}$,
其中转移矩阵 $\mx{A}$ 为:
|
\begin{equation}
\mx{A} =
\begin{pmatrix}
0 & 1 & 1/2 & 1 \\
1/2 & 0 & 1/2 & 0 \\
1/2 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{pmatrix} .
\end{equation}
|
(10.1)
|
第一列有两个非零项。如果你在主页 $1$ 上,有两个链接:一个到页面 2,一个到页面 3。因此以概率 $0.5$ 进入主页 2,以概率 $0.5$ 进入主页 3。类似地,第 $j$ 列的各项取决于主页 $j$ 上有哪些链接。
针对页面问题,通常按如下方式修正概率:以概率 $0.15$ 均匀随机跳转到任意主页,以概率 $0.85$ 根据链接选择下一个主页。此时转移矩阵变为:
|
\begin{equation}
\mx{B} =
0.15
\begin{pmatrix}
1/4 & 1/4 & 1/4 & 1/4 \\
1/4 & 1/4 & 1/4 & 1/4 \\
1/4 & 1/4 & 1/4 & 1/4 \\
1/4 & 1/4 & 1/4 & 1/4
\end{pmatrix}
+ 0.85
\begin{pmatrix}
0 & 1 & 1/2 & 1 \\
1/2 & 0 & 1/2 & 0 \\
1/2 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{pmatrix} .
\end{equation}
|
(10.2)
|
各页面的与所谓的平稳概率向量 $\vc{p}$ 相关,它满足
|
\begin{equation}
\mx{B} \vc{p } = \vc{p} .
\end{equation}
|
(10.3)
|
这是未知量为 $\vc{p}$ 的方程,可以用计算;同时它也与本章讨论的概念相关。
在本例中,向量 $\vc{p}$ 为
|
\begin{equation}
\vc{p} =
\begin{pmatrix}
p_1\\
p_2\\
p_3\\
p_4
\end{pmatrix}
=
\begin{pmatrix}
0.43\\
0.31\\
0.22\\
0.04
\end{pmatrix}
\end{equation}
|
(10.4)
|
显然,'Immersive Math' 应当是首选。
关于如何在超大网络(如互联网)上求解页面问题,我们将在
例 10.12中结合本章关于与的内容继续讨论。
我们先给出与的定义。
定义 10.1:
特征值与特征向量
设 $\mx{A}$ 为方阵。若非零$\vc{v}$ 满足 $\mx{A}\vc{v}$ 与 $\vc{v}$ 平行,即存在标量 $\lambda$ 使得
|
\begin{equation}
\mx{A}\vc{v} = \lambda \vc{v} .
\end{equation}
|
(10.5)
|
此时标量 $\lambda$ 称为。
在
第 9 章中我们看到,可以表示为矩阵乘法。对于同样可以定义与:对线性映射 $F$,若非$\vc{v}$ 满足 $F(\vc{v})$ 与 $\vc{v}$ 平行,即 $F(\vc{v}) = \lambda \vc{v}$,则称 $\vc{v}$ 为特征向量;相应的 $\lambda$ 称为特征值。
例 10.3:
寻找特征向量游戏
需要注意:对于或变换,在不知坐标系的情况下也能被良好定义。下面的例子与交互插图展示了这一基本概念,可视作一个“寻找特征向量”的小游戏。
在
交互插图 10.3中,
我们还计算 $\frac{\ln{ F(\vc{v}) } }{\ln{\vc{v}}}$。
试着通过交互移动输入向量 ${\vc{v}}$,看看能找到多少个,并尝试为每个特征向量确定其。
在
交互插图 10.3中,
你可能注意到,改变向量 $\vc{v}$ 的并不会改变它是否是这一事实。这源于该的线性性,见下述定理。
定理 10.1:
若 $\vc{v}$ 是特征值为 $\lambda$ 的,则对任意 $\mu \neq 0$,$\mu \vc{v}$ 也是具有相同的特征向量。
若 $\vc{v}$ 是且其为 $\lambda$,则 $\vc{v} \neq 0$ 且
$F(\vc{v}) = \lambda \vc{v}$。对任意非零倍数 $\vc{u} = \mu \vc{v}$,有 $\vc{u} \neq 0$ 且
$F(\vc{u}) = F( \mu \vc{v}) = \mu F(\vc{v}) = \mu \lambda \vc{v} = \lambda \vc{u}$。因此定理成立。
$\square$
因此,总可以按比例缩放。然而,请记住必须是非零向量。
例 10.4:
线性函数的最大伸长
在
例 10.3中,我们以交互方式展示了与。一个有趣的问题是研究线性映射 $F$ 的输出 $F(\vc{v})$ 相对输入向量 $\vc{v}$ 能变大多少。下图中我们将输入向量 $\vc{v}$ 的固定为 1。你可以通过图下方的滑块旋转输入向量。注意输出向量 $F(\vc{v})$ 的端点位于一个椭圆上。存在一个方向使伸长最大,而与该方向垂直的方向会得到最小的伸长。稍后在本章(
第 10.6 节)我们将看到其原因,并说明如何计算这些方向。
本节将介绍如何计算与。(注意:该方法基于求多项式的根。在实际中,存在更高效的数值方法用于求与。随后我们还会利用与根之间的联系,用特征值来计算根,而非反过来。)
定义 10.2:
特征多项式
设 $\mx{A}$ 为大小为 $n \times n$ 的方阵。如下多项式
|
\begin{equation}
p_{\mx{A}}(\lambda) = \det(\lambda I - \mx{A})
\end{equation}
|
(10.6)
|
上式称为
。
定理 10.2:
关于 $\lambda$ 是 $n$ 次多项式。
矩阵 $\mx{A}$ 的$\lambda$是特征多项式 $p_{\mx{A}}(\lambda)$ 的各根。
给定矩阵 $\mx{A}$,如何计算其$\vc{v}$及其对应$\lambda$?如下方程:
|
\begin{equation}
\mx{A}\vc{v} = \lambda \vc{v} , \vc{v} \neq 0
\end{equation}
|
(10.7)
|
可改写为
|
\begin{equation}
\lambda \vc{v} - \mx{A}\vc{v} = ( \lambda I - \mx{A} ) \vc{v} = 0.
\end{equation}
|
(10.8)
|
若 $\vc{v}$ 是,则矩阵 $(\lambda I - \mx{A})$ 的零空间包含一个非零。根据
定理 7.10,这意味着 $p_{\mx{A}}(\lambda) = \det( \lambda I - \mx{A} ) = 0$。
由此可知,正是的各根。反过来,对于特征多项式的任一根 $\lambda$,方程 $( \lambda I - \mx{A} ) \vc{v} = 0$ 都存在非零解 $\vc{v}$;这给出了一个,因为有 $\mx{A}\vc{v} = \lambda \vc{v}$。
$\square$
例 10.5:
使用特征多项式计算特征值与特征向量
计算下列矩阵的与:
|
\begin{equation}
\mx{A} = \begin{pmatrix}
5/2 & -3/4 \\
2 & 0
\end{pmatrix} .
\end{equation}
|
(10.9)
|
这些是的各根:
|
\begin{equation}
\det( \lambda I - \mx{A} ) =
\begin{vmatrix}
\lambda -5/2 & 3/4 \\
-2 & \lambda
\end{vmatrix} = (\lambda-\frac{5}{2}) (\lambda) - \frac{3}{4}(-2) =
\lambda^2 - \frac{5}{2}\lambda + \frac{3}{2} = 0 .
\end{equation}
|
(10.10)
|
方程 $\lambda^2 - \frac{5}{2}\lambda + \frac{3}{2} = 0$ 的两个根为
|
\begin{equation}
\lambda_{1,2} = \frac{5}{4} \pm \sqrt{ \frac{25}{4}-\frac{3}{2}} = \frac{5}{4} \pm \frac{1}{4} .
\end{equation}
|
(10.11)
|
因此两个为 $\lambda_1 = 1$ 与 $\lambda_2 = 3/2$。
对每个,可通过求解下式得到对应的:
$( \lambda I - \mx{A} ) \vc{v} = 0$.
对于 $\lambda_1 = 1$,有
|
\begin{equation}
(1 I - \mx{A}) \vc{v} = \begin{pmatrix}
-3/2 & 3/4 \\
-2 & 1
\end{pmatrix} \vc{v} = 0 .
\end{equation}
|
(10.12)
|
该方程组的参数解为
|
\begin{equation}
\vc{v} = t \begin{pmatrix}
1\\
2
\end{pmatrix} .
\end{equation}
|
(10.13)
|
因此所有向量
|
\begin{equation}
\vc{v} = t \begin{pmatrix}
1\\
2
\end{pmatrix} , \quad t \neq 0
\end{equation}
|
(10.14)
|
都是对应 $1$ 的。需注意必须令 $t \neq 0$,因为按定义不是。
对于 $\lambda_2 = 3/2$,有
|
\begin{equation}
(\frac{3}{2} I - \mx{A}) \vc{v} = \begin{pmatrix}
-1 & 3/4 \\
-2 & 3/2
\end{pmatrix} \vc{v} = 0 .
\end{equation}
|
(10.15)
|
该方程组的参数解为
|
\begin{equation}
\vc{v} = t \begin{pmatrix}
3\\
4
\end{pmatrix} .
\end{equation}
|
(10.16)
|
因此所有向量
|
\begin{equation}
\vc{v} = t \begin{pmatrix}
3\\
4
\end{pmatrix} , \quad t \neq 0
\end{equation}
|
(10.17)
|
是对应 $3/2$ 的。
交互插图 10.5展示了该。通过移动红色输入箭头,可直观“验证”这些向量确为,因为蓝色输出向量将与红色输入向量平行。
与与对角化这一概念密切相关。
其核心思想是:若选择作为向量,则会变得格外简单。我们需要针对与矩阵分别给出对角化的定义;两者本质上是等价的。
关于第一个定义,需要回忆:即使不选取,也可以定义$F(\vc{v})$。例如,将输入向量拉长两倍的,与是否选取无关。然而,一旦为该选定了,便可将其写成 $F(\vc{v}) = \mx{A}\vc{v}$ 的形式,其中 $\mx{A}$ 是变换矩阵,且取决于所选的。基于此,我们可以给出的可对角化定义。
定义 10.3:
若存在某个使得变换矩阵为对角矩阵,则称$F$可对角化。
定义 10.4:
若存在可逆矩阵 $\mx{V}$ 与对角矩阵 $\mx{D}$ 满足下式,则称矩阵 $\mx{A}$ 可对角化:
|
\begin{equation}
\mx{A} = \mx{V} \mx{D} \mx{V}^{-1} .
\end{equation}
|
(10.18)
|
矩阵 $\mx{A}$ 被分解为三个矩阵 $\mx{V}$、$\mx{D}$ 与 $\mx{V}^{-1}$ 的乘积。此类分解在诸多应用中极为有用;我们将在本章后续给出若干示例。
为理解对角化与、之间的关系,我们将矩阵方程重写为:
|
\begin{equation}
\mx{A} \mx{V}= \mx{V} \mx{D} .
\end{equation}
|
(10.19)
|
设 $\mx{V}$ 的为 $(\vc{v}_1, \ldots, \vc{v}_n)$,而 $\mx{D}$ 的对角元为 $(\lambda_1, \ldots, \lambda_n)$。
据此可将上式写为:
|
\begin{equation}
\mx{A}
\begin{pmatrix}
\vc{v}_1 & \ldots & \vc{v}_n
\end{pmatrix}
= \begin{pmatrix}
\vc{v}_1 & \ldots & \vc{v}_n
\end{pmatrix}
\mx{D}
\end{equation}
|
(10.20)
|
或等价地
|
\begin{equation}
\begin{pmatrix}
\mx{A} \vc{v}_1 & \ldots & \mx{A} \vc{v}_n
\end{pmatrix}
= \begin{pmatrix}
\lambda_1 \vc{v}_1 & \ldots & \lambda_n \vc{v}_n
\end{pmatrix}.
\end{equation}
|
(10.21)
|
换言之,矩阵方程的第 $k$ 列可写为:
|
\begin{equation}
\mx{A} \vc{v}_k = \lambda_k \vc{v}_k,
\end{equation}
|
(10.22)
|
因此,$\mx{V}$ 的各列是 $\mx{A}$ 的,其对应的位于 $\mx{D}$ 的相应对角元上。
可将上述内容总结为如下定理。
定理 10.3:
矩阵 $\mx{A}$ 可对角化当且仅当存在由构成的。
此外,在分解 $ \mx{A} = \mx{V} \mx{D} \mx{V}^{-1}$ 中,$\mx{V}$ 的列对应,$\mx{D}$ 的对角元对应。
例 10.6:
单根与可对角化矩阵
判断下列矩阵是否可对角化;若可,计算矩阵 $\mx{V}$ 与 $\mx{D}$ 使得
|
\begin{equation}
\mx{A} = \begin{pmatrix}
5/2 & -3/4 \\
2 & 0
\end{pmatrix}
\end{equation}
|
(10.23)
|
并且满足
|
\begin{equation}
\mx{A} = \mx{V} \mx{D} \mx{V}^{-1} .
\end{equation}
|
(10.24)
|
在前一个例子中,我们找到了两个的
|
\begin{equation}
\vc{v} _1= \begin{pmatrix}
1\\
2
\end{pmatrix} \spc \text{以及} \spc \vc{v} _2= \begin{pmatrix}
3\\
4
\end{pmatrix}
\end{equation}
|
(10.25)
|
其为 $\lambda_1 = 1$ 与 $\lambda_2 = 3/2$。根据
定理 10.3,
$\mx{A}$ 可分解为
|
\begin{equation}
\mx{V} = \begin{pmatrix}
1 & 3 \\
2 & 4
\end{pmatrix}
\end{equation}
|
(10.26)
|
以及
|
\begin{equation}
\mx{D} = \begin{pmatrix}
1 & 0 \\
0 & \frac{3}{2}
\end{pmatrix} .
\end{equation}
|
(10.27)
|
对 $2 \times 2$ 矩阵,为二次,因此有两个根(计入复数根并考虑重数)。在
例 10.5中,这两个根($2$ 与 $3$)不同,因而存在由构成的。对于一般的 $n \times n$ 矩阵,也成立,见下述定理。
定理 10.4:
若 $n \times n$ 矩阵 $\mx{A}$ 拥有 $n$ 个彼此不同的,则 $\mx{A}$ 可对角化。此外,属于不同的 $n$ 个总是。
记这 $n$ 个不同的为 $\lambda_1, \ldots, \lambda_n$。对应每个$\lambda_k$,至少存在一个$\vc{v}_k$。
若这 $n$ 个,则它们构成一个。由
定理 10.3,此时矩阵 $\mx{A}$ 可对角化。因此我们只需证明这 $n$ 个。
为此我们对的个数 $k$ 作递归。当 $k=2$ 时结论成立,因为平行的两个向量具有相同的。假设 $k-1$ 个具有不同的总是,我们需要证明对于 $k$ 个具有不同的,方程
|
\begin{equation}
z_1 \vc{v}_1 + z_2 \vc{v}_2 + \ldots + z_k \vc{v}_k = 0
\end{equation}
|
(10.28)
|
仅有一个解,即 $z_1 = z_2 = \ldots = z_k = 0$。
两边同乘以 $\mx{A}$,得到
|
\begin{equation}
\mx{A} (z_1 \vc{v}_1 + z_2 \vc{v}_2 + \ldots + z_k \vc{v}_k) =
z_1 \mx{A} \vc{v}_1 + z_2 \mx{A}\vc{v}_2 + \ldots + z_k \mx{A}\vc{v}_k =
z_1 \lambda_1 \vc{v}_1 + z_2 \lambda_2 \vc{v}_2 + \ldots + z_k \lambda_k \vc{v}_k =
0 .
\end{equation}
|
(10.29)
|
将此式减去原式的 $ \lambda_k $ 倍,得到
|
\begin{equation}
z_1 (\lambda_1-\lambda_k) \vc{v}_1 + z_2 (\lambda_2 -\lambda_k) \vc{v}_2 + \ldots + z_{k-1} (\lambda_{k-1} - \lambda_k) \vc{v}_{k-1}
= 0 .
\end{equation}
|
(10.30)
|
由于具有不同的 $k-1$ 个总是,于是有
|
\begin{equation}
\begin{array}{ll}
z_1 (\lambda_1-\lambda_k) & = 0 \\
z_2 (\lambda_2-\lambda_k) & = 0 \\
& \vdots \\
z_{k-1} (\lambda_{k-1} - \lambda_k) & = 0.
\end{array}
\end{equation}
|
(10.31)
|
由于所有均不同,故 $z_1 = z_2 = \ldots = z_{k-1} = 0$。
将其代入原方程,得到 $z_k \vc{v}_k = 0$,从而 $z_k= 0$。
证毕。
$\square$
因此当所有根互不相同时,矩阵可对角化。若存在更高重数的根,矩阵既可能可对角化(见
例 10.7),也可能不可对角化(见
例 10.8)。
例 10.7:
重根与可对角化矩阵
判断下列矩阵是否可对角化;若可,计算矩阵 $\mx{V}$ 与 $\mx{D}$ 使得
|
\begin{equation}
\mx{A} = \begin{pmatrix}
2 & 0\\
0 & 2
\end{pmatrix}
\end{equation}
|
(10.32)
|
并且满足
|
\begin{equation}
\mx{A} = \mx{V} \mx{D} \mx{V}^{-1} .
\end{equation}
|
(10.33)
|
这个例子略显简单,因为矩阵 $\mx{A}$ 已经是对角矩阵;但它仍能说明即使具有重根,矩阵也可能可对角化。尽管显然可对角化,我们仍将完成相关计算。
与
例 10.5相同,先求。
这些是的各根:
|
\begin{equation}
\det( \lambda I - \mx{A} ) =
\mx{A} = \begin{vmatrix}
\lambda - 2 & 0\\
0 & \lambda -2
\end{vmatrix} = (\lambda-2) (\lambda-2) - (0)(0) =
(\lambda-2) (\lambda-2) = 0 .
\end{equation}
|
(10.34)
|
该多项式在 $\lambda = 2$ 处有一个重根。
对于$\lambda = 2$,有
|
\begin{equation}
(2 I - \mx{A}) \vc{v} = \begin{pmatrix}
0 & 0 \\
0 & 0
\end{pmatrix} \vc{v} = 0 .
\end{equation}
|
(10.35)
|
该方程组的参数解为
|
\begin{equation}
\vc{v} = t_1\begin{pmatrix}
1\\
0
\end{pmatrix} + t_2 \begin{pmatrix}
0\\
1
\end{pmatrix} .
\end{equation}
|
(10.36)
|
在此情形下可以找到由构成的,例如:
|
\begin{equation}
\vc{v}_1 = \begin{pmatrix}
1\\
0
\end{pmatrix}
\end{equation}
|
(10.37)
|
以及
|
\begin{equation}
\vc{v}_1 = \begin{pmatrix}
0\\
1
\end{pmatrix} .
\end{equation}
|
(10.38)
|
因此该矩阵可对角化。
事实上这并不令人意外,因为矩阵 $\mx{A}$ 本身就是对角矩阵。因此无需计算,我们即可令 $\mx{D} = \mx{A}$、$\mx{V} = \mx{I}$、$\mx{V}^{-1} = \mx{I}^{-1} = \mx{I}$,并写出:
|
\begin{equation}
\mx{A} = \mx{I}\mx{A}\mx{I}^{-1} = \mx{V} \mx{D} \mx{V}^{-1}.
\end{equation}
|
(10.39)
|
例 10.8:
重根与不可对角化矩阵
判断下列矩阵是否可对角化;若可,计算矩阵 $\mx{V}$ 与 $\mx{D}$ 使得
|
\begin{equation}
\mx{A} = \begin{pmatrix}
1 & 1\\
0 & 1
\end{pmatrix}
\end{equation}
|
(10.40)
|
并且满足
|
\begin{equation}
\mx{A} = \mx{V} \mx{D} \mx{V}^{-1} .
\end{equation}
|
(10.41)
|
与
例 10.5类似,我们先确定。
这些是的各根:
|
\begin{equation}
\det( \lambda I - \mx{A} ) =
\mx{A} = \begin{vmatrix}
\lambda - 1 & -1\\
0 & \lambda -1
\end{vmatrix} = (\lambda-1) (\lambda-1) - (0)(-1) =
(\lambda-1) (\lambda-1) = 0 .
\end{equation}
|
(10.42)
|
该多项式在 $\lambda = 1$ 处有一个重根。
对于$\lambda = 1$,有
|
\begin{equation}
(1 I - \mx{A}) \vc{v} = \begin{pmatrix}
0 & -1 \\
0 & 0
\end{pmatrix} \vc{v} = 0 .
\end{equation}
|
(10.43)
|
该方程组的参数解为
|
\begin{equation}
\vc{v} = t \begin{pmatrix}
1\\
0
\end{pmatrix} .
\end{equation}
|
(10.44)
|
因此所有向量
|
\begin{equation}
\vc{v} = t \begin{pmatrix}
1\\
0
\end{pmatrix} , \quad t \neq 0
\end{equation}
|
(10.45)
|
是对应$1$的。
这些是仅有的;任意选取其中两个都是的。这意味着该矩阵不可对角化。
在
例 10.6中,只有单根,因此所有均不同。由
定理 10.4可知,此类矩阵总是可对角化。对于具有重根(或更高重数)的矩阵,既可能如
例 10.7那样可对角化,也可能如
例 10.8那样不可对角化。是否可对角化取决于对每个$\lambda$,能从 $(\lambda I - \mx{A})$ 的零空间中选出多少个的。
在此引入代数重数与的概念会很有用。
定义 10.5:
代数重数、特征子空间与几何重数
设 $\lambda$ 为矩阵 $\mx{A}$ 的一个。$\lambda$ 关于的重数称为 $\lambda$ 的。$(\lambda I - \mx{A})$ 的零空间称为与$\lambda$相关的矩阵 $\mx{A}$ 的。$\lambda$ 的是 $(\lambda I - \mx{A})$ 的零空间的维数,即该的维数。
定理 10.5:
某个 $\lambda$ 的 总是不大于其 。
假设特征值 $\lambda_0$ 的为 $k$。这意味着
$(\lambda_0 I - \mx{A})$ 的维数为 $k$;换言之,我们可以找到 $k$ 个的$\vc{e}_1, \ldots, \vc{e}_k$
它们对应$\lambda_0$。据此选取新的$\vc{e}_1, \ldots, \vc{e}_k, \ldots, \vc{e}_n$,使前 $k$
个向量由 $\lambda_0$ 的给出。在该新下,变换矩阵 $\mx{A}$ 具有如下形式:
|
\begin{equation}
\mx{A} =
\begin{pmatrix}
\lambda_0 & 0 & \ldots & 0 & a_{1,k+1} & \ldots & a_{1,n}\\
0 & \lambda_0 & \ldots & 0 & a_{2,k+1} & \ldots & a_{2,n}\\
\vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\
0 & 0 & \ldots & \lambda_0 & a_{k,k+1} & \ldots & a_{k,n}\\
\vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\
0 & 0 & \ldots & 0 & a_{n,k+1} & \ldots & a_{n,n}\\
\end{pmatrix}
\end{equation}
|
(10.46)
|
该矩阵的可写作 $(\lambda - \lambda_0)^k p(\lambda)$,因此至少为 $k$。这表明总是不大于。
$\square$
定理 10.6:
矩阵 $\mx{A}$ 可对角化,当且仅当每个的与一致。
等价地,对 $n \times n$ 矩阵 $\mx{A}$,若各的维数之和为 $n$,则 $\mx{A}$ 可对角化。
设存在 $k$ 个不同的 $\lambda_1, \ldots, \lambda_k$。
若每个特征值的与一致,记该重数为 $m_i$。由代数重数可知 $\sum_{i=1}^k m_i = n$。由于几何重数为 $m_i$,可得 $m_i$ 个线性无关的 $\vc{v}_{i,1}, \ldots, \vc{v}_{i,m_i}$。
将所有特征值对应的这些收集起来,$\{ \vc{v}_{1,1}, \ldots, \vc{v}_{1,m_1}, \ldots, \vc{v}_{k,1}, \ldots, \vc{v}_{k,m_k} \}$ 共计 $n$ 个向量。我们将通过证明它们来说明它们构成一组。
设存在标量 $c_{i,j}$,其中 $1 \leq i \leq k$ 且 $1 \leq j \leq m_i$,使得
|
\begin{equation}
\sum_{i=1}^k \sum_{j=1}^{m_i} c_{i,j} \vc{v}_{i,j} = 0 .
\end{equation}
|
(10.47)
|
构造向量
|
\begin{equation}
\vc{w}_{i} = \sum_{j=1}^{m_i} c_{i,j} \vc{v}_{i,j}.
\end{equation}
|
(10.48)
|
对每个 $i$,向量 $\vc{w}_i$ 要么为零,要么是对应$\lambda_i$的。
若至少有一个不为零,则得到如下求和形式:
|
\begin{equation}
\sum_{i=1}^k \vc{w}_i= 0
\end{equation}
|
(10.49)
|
由对应不同的组成。然而根据
定理 10.4,这些向量必然,故它们之和为零的唯一可能是各向量均为零。
由此得到
|
\begin{equation}
\vc{w}_{i} = \sum_{j=1}^{m_i} c_{i,j} \vc{v}_{i,j} = 0 .
\end{equation}
|
(10.50)
|
由于对每个 $i$,集合 $\{\vc{v}_{i,1}, \ldots, \vc{v}_{i,m_i}\}$ 均,于是有
|
\begin{equation}
c_{i,j} = 0, \quad 1 \leq i \leq k, 1 \leq j \leq m_i \, .
\end{equation}
|
(10.51)
|
由此可知,$\{ \vc{v}_{1,1}, \ldots, \vc{v}_{1,m_i}, \ldots, \vc{v}_{k,1}, \ldots, \vc{v}_{k,m_k} \}$ 线性无关。因此它们构成一组,从而矩阵 $\mx{A}$ 可对角化。
反向证明:若矩阵可对角化,则几何重数与代数重数必相等。假设 $\mx{A}$ 可对角化,则存在可逆矩阵 $\mx{V}$ 与对角矩阵 $\mx{D}$ 使得 $\mx{A} = \mx{V} \mx{D} \mx{V}^{-1}$。矩阵 $\mx{A}$ 与 $\mx{D}$ 拥有相同的,且对每个 $\lambda_i$ 具有相同的几何重数。易证对角矩阵的几何重数与代数重数相同,证毕。
$\square$
在
例 10.7与
例 10.8中,均只有一个,且两例的均为 2。在
例 10.7中,仅为 1,因此不可对角化;而在
例 10.8中,为 2,因此可对角化。
需要注意的是:对随机矩阵(例如每个元素独立服从分布),不可对角化的概率极小。事实上,若使用真正的连续分布而非(离散的)计算机近似,该概率为零。因此,在某种意义上,不可对角化矩阵是例外。不过,在实际应用中存在具有内在结构而导致不可对角化的矩阵。
我们主要处理实矩阵与实向量,但包含复数的矩阵与向量同样很有用。即便对实矩阵,有时也需要考虑复与复。
对实矩阵与复矩阵 $\mx{A}$,复与复的定义是相似的。
定义 10.6:
复特征值与复特征向量
设 $\mx{A}$ 为实数或复数项的方阵。一个非零的复数项$\vc{v}$称为,当且仅当 $\mx{A}\vc{v}$ 与 $\vc{v}$ 平行;即存在复数标量 $\lambda$,使得
|
\begin{equation}
\mx{A}\vc{v} = \lambda \vc{v} .
\end{equation}
|
(10.52)
|
该标量 $\lambda$ 称为。
对称矩阵的一个有用性质总结如下定理。
定理 10.7:
对称矩阵 $\mx{A}$ 的全部为实数。
设存在一个$\vc{v}$(可能为复数),及其对应的$\lambda$(亦可能为复数)。首先我们证明:
先证明 $z = \bar{\vc{v}}^\T \mx{A} \vc{v}$ 为实数。为此我们使用复数的共轭:若 $z=a+bi$,则其共轭为 $\overline{z}=a-bi$。
于是得到
|
\begin{equation}
\bar{z}= \overline{\bar{\vc{v}}^\T \mx{A} \vc{v}} = \vc{v}^\T \bar{\mx{A}} \bar{\vc{v}} = (\vc{v}^\T \bar{\mx{A}} \bar{\vc{v}})^\T = \bar{\vc{v}} \bar{\mx{A}}^\T \vc{v} = \bar{\vc{v}}^\T \mx{A} \vc{v} = z .
\end{equation}
|
(10.53)
|
由于 $\bar{z}=z$,标量 $z$ 为实数。
现在利用 $\vc{v}$ 是这一事实,可得
|
\begin{equation}
z = \bar{\vc{v}}^\T \mx{A} \vc{v}= \bar{\vc{v}}^\T \lambda \vc{v} = \lambda (\bar{\vc{v}}^\T \vc{v}) .
\end{equation}
|
(10.54)
|
又因为 $\bar{\vc{v}}^\T \vc{v}$ 总为实数,故 $\lambda$ 也为实数。
$\square$
注意在上述证明中我们使用了 $\bar{\mx{A}}^\T = \mx{A}$。因此,对满足约束 $\bar{\mx{A}}^\T = \mx{A}$ 的复矩阵,同样可以证明其所有均为实数。
定理 10.8:
对于对称矩阵 $\mx{A}$,存在矩阵 $\mx{U}$ 与对角矩阵 $\mx{D}$,使得
|
\begin{equation}
\mx{A} = \mx{U} \mx{D} \mx{U}^{-1} = \mx{U} \mx{D} \mx{U}^{T} .
\end{equation}
|
(10.55)
|
换言之,可以使用由构成的来进行对角化。
我们将通过对矩阵 $\mx{A}$ 的规模 $k$ 进行归纳来证明上述结论。
当 $k=1$(即 $1\times 1$ 的矩阵 $\mx{A}$)时,定理成立。此时可取 $\mx{U}=(1)$、$\mx{D}=\mx{A}$。
我们假设该定理对 $(k-1) \times (k-1)$ 的矩阵成立。
设 $\mx{A}$ 为 $n \times n$ 的实对称矩阵。我们将证明可使用由构成的来对角化 $\mx{A}$。至少存在一个$\lambda$及其对应的$\vc{v}$。令 $\vc{q}_1 = \frac{\vc{v}}{||\vc{v}||}$。
任选一个 $k \times k$ 的矩阵 $\mx{Q} = \begin{pmatrix}\vc{q}_1 & \ldots & \vc{q}_k\end{pmatrix}$,其第一列为 $\vc{q}_1$。
将 $\mx{A}$ 与 $\mx{Q}$ 相乘得到
|
\begin{equation}
\mx{A}\mx{Q} =
\begin{pmatrix}
\lambda \vc{q}_1 & \mx{A}\vc{q}_2 & \ldots & \mx{A} \vc{q}_k
\end{pmatrix}
=
\mx{Q}
\begin{pmatrix}
\lambda & \vc{w}^\T \\
0 & \tilde{\mx{A}}
\end{pmatrix} .
\end{equation}
|
(10.56)
|
其中 $\vc{w}$ 为某个 $(k-1) \times 1$ 的,$\tilde{\mx{A}}$ 为某个 $(k-1) \times (k-1)$ 的矩阵。
由此得到
|
\begin{equation}
\mx{Q}^\T \mx{A} \mx{Q} =
\begin{pmatrix}
\lambda & \vc{w}^\T \\
0 & \tilde{\mx{A}}
\end{pmatrix} .
\end{equation}
|
(10.57)
|
由于 $\mx{A}$ 是对称的,故有
|
\begin{equation}
(\mx{Q}^\T \mx{A} \mx{Q})^\T =
\mx{Q}^\T \mx{A}^\T \mx{Q} =
\mx{Q}^\T \mx{A} \mx{Q} =
\begin{pmatrix}
\lambda & 0 \\
\vc{w} & \tilde{\mx{A}}^\T
\end{pmatrix} .
\end{equation}
|
(10.58)
|
这意味着 $\vc{w}=\vc{0}$ 且 $\tilde{\mx{A}}^\T = \tilde{\mx{A}}$。
由归纳假设,$\tilde{\mx{A}}$ 的大小为 $(k-1) \times (k-1)$,可用由构成的基将其对角化。
因此存在 $\tilde{\mx{Q}}$ 与 $\tilde{\mx{D}}$ 使得
|
\begin{equation}
\tilde{\mx{A}} =
\tilde{\mx{Q}} \tilde{\mx{D}} \tilde{\mx{Q}}^\T.
\end{equation}
|
(10.59)
|
于是得到由构成的,其中
|
\begin{equation}
\mx{U} =
\mx{Q}
\begin{pmatrix}
1 & 0 \\
0 & \tilde{\mx{Q}}
\end{pmatrix}
\end{equation}
|
(10.60)
|
以及
|
\begin{equation}
\mx{D} =
\begin{pmatrix}
\lambda & 0 \\
0 & \tilde{\mx{D}}
\end{pmatrix},
\end{equation}
|
(10.61)
|
因此证明完成。
$\square$
定义 10.7:
正定性
设 $\mx{A}$ 为实对称的 $n \times n$ 矩阵,称其为:
|
\begin{align}
\begin{array}{lll}
&(1) & \text{正定:} & \vc{v}^T \mx{A} \vc{v} > 0, \, \, \forall \vc{v} \in R^n \setminus 0 \\
&(2) & \text{半正定:} & \vc{v}^T \mx{A} \vc{v} \geq 0, \, \, \forall \vc{v} \in R^n \setminus 0\\
&(3) & \text{负定:} & \vc{v}^T \mx{A} \vc{v} < 0, \, \, \forall \vc{v} \in R^n \setminus 0\\
&(4) & \text{半负定:} & \vc{v}^T \mx{A} \vc{v} \leq 0, \, \, \forall \vc{v} \in R^n \setminus 0\\
&(5) & \text{不定:} & \vc{v}^T \mx{A} \vc{v} \text{既取正值也取负值} \\
\end{array}
\end{align}
|
(10.62)
|
定理 10.9:
正定性与特征值
设 $\mx{A}$ 为实对称的 $n \times n$ 矩阵,则
|
\begin{align}
\begin{array}{ll}
&(1) & \text{当且仅当所有特征值均为正时,正定} \\
&(2) & \text{当且仅当所有特征值均为非负时,半正定} \\
&(3) & \text{当且仅当所有特征值均为负时,负定} \\
&(4) & \text{当且仅当所有特征值均为非正时,半负定} \\
&(5) & \text{当存在正、负特征值时,不定} \\
\end{array}
\end{align}
|
(10.63)
|
由于矩阵 $\mx{A}$ 是对称的,可用矩阵 $\mx{U}$ 将其对角化,即
$\mx{A} = \mx{U}^\T \mx{D} \mx{U}$.
作坐标变换 $\vc{w} = \mx{U} \vc{v}$,得到
|
\begin{equation}
\vc{v}^T \mx{A} \vc{v} = \vc{v}^T \mx{U}^\T \mx{D} \mx{U} \vc{v} = \vc{w}^T \mx{D} \vc{w}
\end{equation}
|
(10.64)
|
若所有均为正,则显然对任意非$\vc{v}$ 有 $\vc{v}^T \mx{A} \vc{v} > 0$。若某个例如 $\lambda_i$ 为零或为负,则对应的$\vc{v} = \vc{u}_i$ 将给出零或负的结果,因为 $\vc{u}_i^T \mx{A} \vc{u}_i = \vc{u}_i^T \lambda_i \vc{u}_i = \lambda_i \leq 0$。这证明了第一部分,其余结论可用类似方法证明。
$\square$
在
例 10.4中,我们研究了在固定输入向量时输出向量 $F(\vc{v})$ 能有多长。这里我们将使用
定理 10.8 与
定理 10.7 来进一步理解。
给定实矩阵 $\mx{A}$ 及其对应的映射 $F(\vc{v}) = \mx{A} \vc{v}$($\vc{v}$ 为实向量),哪个输入 $\vc{v}$ 能使伸长量 $s = \frac{|| \mx{A} \vc{v}||}{||\vc{v}||}$ 最大或最小?
研究伸长量的平方更为容易,即:
|
\begin{equation}
s^2 =\left(\frac{|| \mx{A} \vc{v}||}{||\vc{v}||}\right)^2= \frac{\vc{v}^\T \mx{A}^\T \mx{A} \vc{v}}{\vc{v}^\T \vc{v}},
\end{equation}
|
(10.65)
|
其中假设向量 $\vc{v}$ 非零。注意此处相关的是矩阵 $\mx{A}^\T \mx{A}$。
该矩阵按构造即为对称。根据
定理 10.8,我们可以使用矩阵 $\mx{U}$ 对其进行对角化,
|
\begin{equation}
\mx{A}^\T \mx{A} = \mx{U} \mx{D} \mx{U}^\T .
\end{equation}
|
(10.66)
|
其为实数。注意 $\mx{A}^\T \mx{A}$ 是半正定矩阵,可由
$ \vc{v}^T \mx{A}^\T \mx{A} \vc{v} = \left( || \mx{A} \vc{v}|| \right)^2 \geq 0$ 看出。由
定理 10.9可知这些均为非负。
为简便起见,假设按 $d_1 \geq d_2 \geq \ldots \geq d_n \geq 0$ 对排序。
于是有
|
\begin{equation}
s^2 = \frac{\vc{v}^\T \mx{A}^\T \mx{A} \vc{v}}{\vc{v}^\T \vc{v}} = \frac{\vc{v}^\T \mx{U} \mx{D} \mx{U}^\T \vc{v}}{\vc{v}^\T \mx{U} \mx{U}^\T \vc{v}} .
\end{equation}
|
(10.67)
|
作坐标变换 $\vc{w} = \mx{U}^\T \vc{v}$,得到
|
\begin{equation}
s^2 = \frac{\vc{w}^\T \mx{D} \vc{w}}{\vc{w}^\T \vc{w}}.
\end{equation}
|
(10.68)
|
为了理解如何最大化该量,注意分子只是
|
\begin{equation}
w_1^2 d_1 + w_2^2 d_2 + \ldots + w_n^2 d_n,
\end{equation}
|
(10.69)
|
其中 $d_1, d_2, \dots, d_n$ 是
$\mx{D}$ 的对角元。此外,分母为
|
\begin{equation}
w_1^2 + w_2^2 + \ldots + w_n^2.
\end{equation}
|
(10.70)
|
因此,直观来看,若希望在尽量减小分母的同时最大化分子,
合理的做法是让第一项占据最大权重,因为 $d_1$ 为最大元素;
例如可令 $w_1 = 1$ 且当 $j\neq1$ 时令 $w_j = 0$。
若希望对上述直觉给出严格证明,可按如下方式进行。首先将
公式 (10.68) 重写为
|
\begin{equation}
s^2 = \frac{\sum_{i=1}^n d_i w_i^2 }{\sum_{i=1}^n w_i^2}.
\end{equation}
|
(10.71)
|
为分析最大值,先通过计算偏导数求所有驻点:
|
\begin{equation}
\frac{\partial (s^2)}{\partial w_i} = \frac{ (2 d_i w_i) (\sum_{i=1}^n w_i^2) - (\sum_{i=1}^n d_i w_i^2 )(2 w_i)}{(\sum_{i=1}^n w_i^2)^2} .
\end{equation}
|
(10.72)
|
由于在驻点处对所有 $i$ 均有 $\frac{\partial (s^2)}{\partial w_i} = 0$,于是得到
|
\begin{equation}
\begin{pmatrix}
d_1 w_1 & w_1 \\
d_2 w_2 & w_2 \\
\vdots & \vdots \\
d_n w_n & w_n
\end{pmatrix}
\begin{pmatrix}
\sum_{i=1}^n w_i^2 \\
\sum_{i=1}^n d_i w_i^2
\end{pmatrix} = \vc{0}.
\end{equation}
|
(10.73)
|
于是得到一个“矩阵乘以向量等于零”的表达式。由于顶端元素是其的平方 $||\vc{w}||^2$,当变换后的向量 $\vc{w}$ 非零时,原向量也非零。因此若 $\vc{w}\neq \vc{0}$,必是该矩阵使表达式为零,即其的维数至少为 1(为 1)。这意味着矩阵的至多为 1,因为
定理 8.8指出与之和等于列数。而
定理 8.9指出等于最大非零的阶数。因此本例中最大的是 $1\times 1$,这进一步意味着每个 $2 \times 2$ 的为零,即:
|
\begin{equation}
\det \begin{pmatrix}
d_i w_i & w_i \\
d_j w_j & w_j
\end{pmatrix} =(d_i-d_j) w_i w_j = 0
\end{equation}
|
(10.74)
|
对所有 $i$ 与 $j$ 均成立。一个可行的解是令 $\vc{w}$ 仅有一个非零元素。
当 $\vc{w}_{max} = \begin{pmatrix} 1 & 0 & \ldots & 0 \end{pmatrix}$ 时取得全局最大伸长量 $d_1$;当 $\vc{w}_{min} = \begin{pmatrix} 0 & 0 & \ldots & 1 \end{pmatrix}$ 时取得全局最小伸长量 $d_n$。
由于 $\vc{w} = \mx{U}^\T \vc{v}$,可得 $\vc{v} = \mx{U} \vc{w}$。这意味着最大伸长量对应 $\vc{v}_1$,即对应最大的 $\mx{A}^\T \mx{A}$ 的;最小伸长量对应 $\vc{v}_n$,即对应最小的 $\mx{A}^\T \mx{A}$ 的。
例 10.9:
对称矩阵的最大伸长
请研究 in
交互插图 10.6,
其中(红色)输入向量的为 1。
尝试改变输入向量 $\vc{v}$,使得输出向量 $F(\vc{v})$ 尽可能长、再尽可能短。本例中的为 $\vc{v} \rightarrow \mx{A} \vc{v}$,其中 $\mx{A}$ 是对称矩阵。在这种情形下,理解会更为直观。
在
第 9 章中,我们看到(有限维)$F$总可以表示为矩阵乘法 $\vc{y} = \mx{A} \vc{x}$。
若该矩阵可对角化,由
定义 10.4知
|
\begin{equation}
\mx{A} = \mx{V} \mx{D} \mx{V}^{-1} .
\end{equation}
|
(10.75)
|
这意味着,若按 $ \vc{x} = \mx{V} \tilde{\vc{x}}$(因此也有 $\vc{y} = \mx{V} \tilde{\vc{y}}$)进行坐标变换,则在新坐标系中得到更简单的关系 $\tilde{\vc{y}} = \tilde{\mx{A}} \tilde{\vc{x}}$,即:
|
\begin{equation}
\tilde{\vc{y}} = \mx{V}^{-1} \vc{y} = \mx{V}^{-1} \mx{V} \mx{D} \mx{V}^{-1} \vc{x} =
\mx{V}^{-1} \mx{V} \mx{D} \mx{V}^{-1} \mx{V} \tilde{\vc{x}}
\end{equation}
|
(10.76)
|
从而
|
\begin{equation}
\tilde{\vc{y}} = \mx{D} \tilde{\vc{x}} .
\end{equation}
|
(10.77)
|
这表示该现由包含的对角矩阵表示。
本例中矩阵 $\mx{A}$ 为
|
\begin{equation}
\mx{A} = \frac{1}{10}\left(\begin{array}{cc}
8 & 6\\
6 & 17\\
\end{array}\right).
\end{equation}
|
(10.78)
|
一般情况下(见上文),给出最大伸长的是 $\mx{A}^T \mx{A}$ 的;但由于此处矩阵是对称的,$\mx{A}$ 的同时也是 $\mx{A}^T \mx{A} = \mx{A}^2$ 的。
本节给出一些关于与的有用结论与性质。
定理 10.10:
若 $\vc{v}$ 是矩阵 $\mx{A}$ 的,其为 $\lambda$;同时也是矩阵 $\mx{B}$ 的,其为 $\mu$,则
|
\begin{equation}
\begin{array}{ll}
(i) & \text{向量}\ \vc{v} \ \text{是矩阵}\ c\mx{A}\ \text{的特征向量,其特征值为}\ c\lambda. \\
(ii) & \text{向量}\ \vc{v} \ \text{是矩阵}\ \mx{A}+d \mx{I}\ \text{的特征向量,其特征值为}\ \lambda+d. \\
(iii) & \text{向量}\ \vc{v} \ \text{是矩阵}\ \mx{A}^n\ \text{的特征向量,其特征值为}\ \lambda^n. \\
(iv) & \text{若}\ \mx{A}\ \text{可逆,向量}\ \vc{v} \ \text{是矩阵}\ \mx{A}^{-1}\ \text{的特征向量,其特征值为}\ 1/\lambda. \\
(v) & \text{向量}\ \vc{v} \ \text{是矩阵}\ \mx{A}+\mx{B}\ \text{的特征向量,其特征值为}\ \lambda + \mu. \\
\end{array}
\end{equation}
|
(10.79)
|
上述多数结论的证明都较为直接。
$(i)$:用矩阵 $c\mx{A}$ 乘以向量 $\vc{v}$。
|
\begin{equation}
(c \mx{A}) \vc{v}= c \mx{A} \vc{v} = c \lambda \vc{v} = (c \lambda) \vc{v} .
\end{equation}
|
(10.80)
|
这证明了 $\vc{v}$ 是 $c \mx{A}$ 的,其为 $c \lambda$。
$(ii)$:用矩阵 $\mx{A} + d\mx{I}$ 乘以向量 $\vc{v}$。
|
\begin{equation}
(\mx{A} + d\mx{I}) \vc{v} = \mx{A}\vc{v} + d \mx{I} \vc{v} = \lambda \vc{v} + d \vc{v} = (\lambda + d) \vc{v} .
\end{equation}
|
(10.81)
|
这证明了 $\vc{v}$ 是 $\mx{A}+d\mx{I}$ 的,其为 $\lambda+d$。
$(iii)$:用矩阵 $\mx{A}^n$ 乘以向量 $\vc{v}$。
|
\begin{equation}
\mx{A}^n \vc{v} = \mx{A}^{n-1} \mx{A} \vc{v} = \lambda \mx{A}^{n-1} \vc{v} = \lambda^2 \mx{A}^{n-2} \vc{v} = \ldots = \lambda^n \vc{v} .
\end{equation}
|
(10.82)
|
这证明了 $\vc{v}$ 是 $\mx{A}^n$ 的,其为 $\lambda^n$。
$(iv)$:考察方程
|
\begin{equation}
\mx{A} \vc{v} = \lambda \vc{v} .
\end{equation}
|
(10.83)
|
若 $\mx{A}$ 可逆,可左乘其逆矩阵。由此得到
|
\begin{equation}
\vc{v} = \lambda \mx{A}^{-1} \vc{v} .
\end{equation}
|
(10.84)
|
由于可逆矩阵的所有均非零,可两边同时除以 $\lambda$,得到
|
\begin{equation}
\frac{1}{\lambda} \vc{v} = \mx{A}^{-1} \vc{v} .
\end{equation}
|
(10.85)
|
这证明了 $\vc{v}$ 是 $\mx{A}^{-1}$ 的,其为 $\frac{1}{\lambda}$。
$(v)$:用矩阵 $\mx{A}+\mx{B}$ 乘以向量 $\vc{v}$。
|
\begin{equation}
( \mx{A} + \mx{B}) \vc{v} = \mx{A} \vc{v} + \mx{B} \vc{v} = \lambda \vc{v} + \mu \vc{v} = (\lambda + \mu) \vc{v} .
\end{equation}
|
(10.86)
|
这证明了 $\vc{v}$ 是 $\mx{A}+\mx{B}$ 的,其为 $\lambda+\mu$。
$\square$
定理 10.11:
矩阵 $\mx{A}$ 与 $\mx{A}^\T$ 具有相同的,即 $p_{\mx{A}}(\lambda) = p_{\mx{A}^\T}(\lambda)$。
这由行列式的性质可得(
定理 7.1)。
|
\begin{equation}
p_{\mx{A}^\T}(\lambda) = \det( \lambda \mx{I} - \mx{A}^\T ) = \det( (\lambda \mx{I} - \mx{A})^\T ) = \det(\lambda \mx{I} - \mx{A}) = p_\mx{A}(\lambda) .
\end{equation}
|
(10.87)
|
$\square$
因此 $ \mx{A}$ 与 $\mx{A}^\T$ 具有相同的。但其可能不同。
定理 10.12:
若 $\mx{V}$ 为可逆矩阵,则矩阵 $\mx{A}$ 与 $\mx{V} \mx{A} \mx{V}^{-1}$ 的特征多项式相同,即 $p_{\mx{A}}(\lambda) = p_{\mx{V} \mx{A} \mx{V}^{-1}}(\lambda)$。
这也由行列式的性质可得(
定理 7.1)。我们可以写 $\mx{I} = \mx{V}\mx{V}^{-1} = \mx{V}\mx{I}\mx{V}^{-1}$,因此
|
\begin{equation}
p_{\mx{V} \mx{A} \mx{V}^{-1}}(\lambda) = \det( \lambda \mx{I} - \mx{V} \mx{A} \mx{V}^{-1} ) =
\det( \lambda \mx{V}\mx{I}\mx{V}^{-1} - \mx{V} \mx{A} \mx{V}^{-1} ).
\end{equation}
|
(10.88)
|
从左侧提取 $\mx{V}$、从右侧提取 $\mx{V}^{-1}$ 得
|
\begin{equation}
p_{\mx{V} \mx{A} \mx{V}^{-1}}(\lambda) =
\det( \mx{V} (\lambda \mx{I} - \mx{A}) \mx{V}^{-1} ) =
\det( \mx{V}) \det(\lambda \mx{I} - \mx{A}) \det(\mx{V}^{-1} ) = \det(\lambda \mx{I} - \mx{A}) = p_{\mx{A}}(\lambda),
\end{equation}
|
(10.89)
|
其中使用了 $\det(\mx{A}\mx{B}) = \det(\mx{A})\det(\mx{B})$ 与 $\det(\mx{V}^{-1}) = \frac{1}{\det(\mx{V})}$ 这两个事实。
$\square$
定理 10.13:
若 $\mx{A}$ 为 $n \times n$ 矩阵,且其为 $\lambda_1, \ldots, \lambda_n$,则
|
\begin{equation}
\det(\mx{A}) = \lambda_1 \cdot \lambda_2 \cdot \ldots \cdot \lambda_n .
\end{equation}
|
(10.90)
|
并且
|
\begin{equation}
\tr(\mx{A}) = \lambda_1 + \lambda_2 + \ldots + \lambda_n .
\end{equation}
|
(10.91)
|
换言之,行列式等于各的乘积;迹(定义为矩阵对角元之和)等于各之和。
这两个定理的证明可通过两种角度考察得到。
一方面,特征多项式为:
|
\begin{equation}
p_{\mx{A}}(\lambda) = (\lambda-\lambda_1) (\lambda-\lambda_2) \cdot (\lambda - \lambda_n) =
\lambda^n - (\lambda_1 + \lambda_2 + \cdot + \lambda_n) \lambda^{n-1} + \ldots + (\lambda_1 \lambda_2 \ldots \lambda_n) (-1)^n .
\end{equation}
|
(10.92)
|
另一方面,特征多项式为:
|
\begin{equation}
p_{\mx{A}}(\lambda) = \det( \lambda \mx{I} - \mx{A} ) = \lambda^n - (a_{11} + a_{22} + \ldots + a_{nn}) \lambda^{n-1} + \ldots + (\det(\mx{A})) (-1)^n
\end{equation}
|
(10.93)
|
或
|
\begin{equation}
p_{\mx{A}}(\lambda) = \det( \lambda \mx{I} - \mx{A} ) = \lambda^n - \tr(\mx{A}) \lambda^{n-1} + \ldots + (\det(\mx{A})) (-1)^n .
\end{equation}
|
(10.94)
|
由此两式得证。
$\square$
本节通过一组示例展示与的实际用途。
例 10.10:
计算 $\mx{A}^n$
可用对角化来简化并理解 $\mx{A}^n$ 的计算。
若 $\mx{A}$ 可对角化,则 $\mx{A} = \mx{V} \mx{D} \mx{V}^{-1}$。
此时 $\mx{A}^n$ 的计算可改写为
|
\begin{equation}
\mx{A}^n = \mx{V} \mx{D} \mx{V}^{-1} \mx{V} \mx{D} \mx{V}^{-1} \mx{V} \mx{D} \mx{V}^{-1} \ldots \mx{V} \mx{D} \mx{V}^{-1} =
\mx{V} \mx{D} \mx{D} \mx{D} \ldots \mx{D} \mx{V}^{-1} =
\mx{V} \mx{D}^n \mx{V}^{-1}.
\end{equation}
|
(10.95)
|
换言之,利用分解可以显式写出 $\mx{A}^n$ 的计算式。
例 10.11:
计算 $\mx{A}^n$
求:
|
\begin{equation}
\begin{pmatrix}
0.68 & -0.24 \\
-0.24 & 0.82
\end{pmatrix}^n?
\end{equation}
|
(10.96)
|
当 $n \rightarrow \infty$ 时会发生什么?
由于该矩阵是对称的,故其为实数,并且可以用矩阵进行对角化。虽然这点在此并非关键,但其分解为:
|
\begin{equation}
\begin{pmatrix}
0.68 & -0.24 \\
-0.24 & 0.82
\end{pmatrix} = \mx{U} \mx{D} \mx{U}^\T =
\begin{pmatrix}
0.8 & -0.6 \\
0.6 & 0.8
\end{pmatrix}
\begin{pmatrix}
0.5 & 0 \\
0 & 1
\end{pmatrix}
\begin{pmatrix}
0.8 & -0.6 \\
0.6 & 0.8
\end{pmatrix}^\T
\end{equation}
|
(10.97)
|
根据前一例,可得:
|
\begin{equation}
\begin{pmatrix}
0.68 & -0.24 \\
-0.24 & 0.82
\end{pmatrix}^n =
\begin{pmatrix}
0.8 & -0.6 \\
0.6 & 0.8
\end{pmatrix}
\begin{pmatrix}
(0.5)^n& 0 \\
0 & 1
\end{pmatrix}
\begin{pmatrix}
0.8 & -0.6 \\
0.6 & 0.8
\end{pmatrix}^\T.
\end{equation}
|
(10.98)
|
当 $n \rightarrow \infty$ 时,$(0.5)^n \rightarrow 0$,于是
|
\begin{equation}
\begin{pmatrix}
0.68 & -0.24 \\
-0.24 & 0.82
\end{pmatrix}^n \rightarrow
\begin{pmatrix}
0.8 & -0.6 \\
0.6 & 0.8
\end{pmatrix}
\begin{pmatrix}
0 & 0 \\
0 & 1
\end{pmatrix}
\begin{pmatrix}
0.8 & -0.6 \\
0.6 & 0.8
\end{pmatrix}^\T =
\begin{pmatrix}
0.36 & -0.48 \\
-0.48 & 0.64
\end{pmatrix} .
\end{equation}
|
(10.99)
|
例 10.12:
PageRank:计算满足 $\mx{B}\vc{p}=\vc{p}$ 的 $\vc{p}$
本章前面我们将网页的重要性()建模为向量 $\vc{p}$,它满足线性方程 $\mx{B}\vc{p} = \vc{p}$。在实际中,直接对方程组 $\mx{B}\vc{p} = \vc{p}$ 做以得到 $\vc{p}$ 通常不可行。
更高效的方法是使用迭代:从任意向量 $\vc{w}_0$ 出发,定义
|
\begin{equation}
\vc{w}_{k+1} = \mx{B} \vc{w}_k .
\end{equation}
|
(10.100)
|
对这类矩阵 $\mx{B}$,可以证明序列 $\vc{w}_k$ 会快速收敛到满足 $\mx{B}\vc{p} = \vc{p}$ 的向量 $\vc{p}$。
为理解这一点,先证明该矩阵具有一个$\vc{v}_1$,其$\lambda_1 = 1$;而其他$\vc{v}_2, \ldots, \vc{v}_n$ 的的绝对均小于 1。
这意味着对任意向量 $\vc{w}_0$,有 $\vc{w}_k = \mx{B}^k \vc{w}_0$,其中
|
\begin{equation}
\vc{w}_k = \mx{B}^k \vc{w}_0 = (\mx{V} \mx{D} \mx{V}^{-1})^k \vc{w}_0 = \mx{V} \mx{D}^k \mx{V}^{-1} \vc{w}_0,
\end{equation}
|
(10.101)
|
其中
|
\begin{equation}
\mx{D}^k=
\begin{pmatrix}
\lambda_1^k & 0 & \ldots & 0 \\
0 & \lambda_2^k & \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & \lambda_n^k \\
\end{pmatrix}
\rightarrow
\begin{pmatrix}
1& 0 & \ldots & 0 \\
0 & 0 & \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & 0 \\
\end{pmatrix},
\end{equation}
|
(10.102)
|
当 $k\rightarrow \infty$ 时。
引入向量 $\vc{e}_1 = \begin{pmatrix} 1 & 0 & \ldots & 0 \end{pmatrix}$。
可见:
|
\begin{equation}
\vc{w}_k = \mx{B}^k \vc{w}_0 \rightarrow \mx{V} \vc{e}_1 \vc{e}_1^\T \mx{V}^{-1} \vc{w}_0 = \vc{v}_1 \mu,
\end{equation}
|
(10.103)
|
其中 $\mx{V} \vc{e}_1 = \vc{v}_1$ 是第一个,未知标量为
$\mu = \vc{e}_1^\T \mx{V}^{-1} \vc{w}_0 $。换言之,选择一个随机向量 $\vc{w}_0$ 并迭代 $\vc{w}_{k+1} = \mx{B} \vc{w}_k$,该向量将收敛到 $\vc{v_1}$ 的某个倍数,
而后者又是 $\vc{p}$ 的某个倍数。
按构造,矩阵 $\mx{B}$ 具有如下性质:若向量 $\vc{w}$ 的各分量均非负且其和为 1,则 $\mx{B} \vc{w}$ 也非负且和为 1;因此从这样的概率向量出发,有 $\vc{w}_k \rightarrow \vc{p}$。
在
例 10.2中,互联网有四个主页,对应的矩阵 $\mx{B}$ 为
|
\begin{equation}
\mx{B} =
0.15
\begin{pmatrix}
1/4 & 1/4 & 1/4 & 1/4 \\
1/4 & 1/4 & 1/4 & 1/4 \\
1/4 & 1/4 & 1/4 & 1/4 \\
1/4 & 1/4 & 1/4 & 1/4
\end{pmatrix}
+ 0.85
\begin{pmatrix}
0 & 1 & 1/2 & 1 \\
1/2 & 0 & 1/2 & 0 \\
1/2 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{pmatrix} .
\end{equation}
|
(10.104)
|
该矩阵的四个分别为 $1$、$0.42$、$-0.42$ 与 $0$。由于各特征值 $\lambda_j$ 的绝对值均小于 $0.5$,每迭代 10 次,误差 $||\vc{w}_k - \vc{p}||$ 将缩小约 1000 倍。
尽管网页数量极其庞大,迭代 $\vc{w}_{k+1} = \mx{B} \vc{w}_k$ 仍是可行的;并且由于只需少量迭代,即可用该方法计算出 $\vc{p}$。
可用于更好地理解。
例 10.13:
理解线性映射
在
例 9.7中,我们研究了将立方体的阴影投射到平面上的。在该例中,计算得到的变换矩阵为
|
\begin{equation}
\mx{A} = \left(\begin{array}{ccc}
1 & -0.5 & 0\\
0 & 0 & 0\\
0 & -0.25 & 1\\
\end{array}\right).
\end{equation}
|
(10.105)
|
与有助于理解该。
其为 $(\lambda-1)^2 \lambda$。对于具有重根的 $\lambda_1 = \lambda_2 = 1$,可选取两组的,如 $\vc{v}_1 = (1, 0, 0)$ 和 $\vc{v}_2 = (0, 0, 1)$。对于 $\lambda_3 = 0$,其为
$\vc{v_3} = t (0.5, 1.0, 0.25), t \neq 0$.
由于前两个张成了 $y=0$,位于该内的所有向量在该下都不受影响。原因在于此类向量 $\vc{x} = (x_1, 0, x_2)$ 可写为两个 $\vc{v}_1$ 与 $\vc{v}_2$ 的:
|
\begin{equation}
\vc{x} = x_1 \vc{v}_1 + x_2 \vc{v}_2,
\end{equation}
|
(10.106)
|
对该向量施加,得到
|
\begin{equation}
\mx{A}\vc{x} = \mx{A}(x_1 \vc{v}_1 + x_2 \vc{v}_2)\\
= x_1 \mx{A}\vc{v}_1 + x_2 \mx{A} \vc{v}_2\\
= x_1 \lambda_1 \vc{v}_1 + x_2 \lambda_2 \vc{v}_2\\
= x_1 \vc{v}_1 + x_2 \vc{v}_2 = \vc{x}.
\end{equation}
|
(10.107)
|
反之,所有与 $\vc{v}_3 = (0.5, 1.0, 0.25)$ 平行的向量都会被映射为:此类向量可写为 $\vc{x} = t \vc{v}_3$,其映射为 $\mx{A}\vc{x} = t\mx{A}\vc{v}_3 = t\lambda_3\vc{v}_3 = t 0 \vc{v}_3 = \vc{0}$。
在
交互插图 10.7中,我们展示如何将其应用于投射阴影。假设物体上某点由向量 $\vc{p}$ 表示。由于这三个彼此,可将向量 $\vc{p}$ 表示为这三个的:
|
\begin{equation}
\vc{p} = \alpha_1 \vc{v}_1 + \alpha_2 \vc{v_2} + \alpha_3 \vc{v_3}.
\end{equation}
|
(10.108)
|
这可理解为:其中两个分量指定了“地面”上的一点(位于某个),另一个分量沿着光源方向。下面看对 $\mx{A}\vc{p}$ 施加后发生了什么:
|
\begin{equation}
\mx{A}\vc{p} = \alpha_1 \mx{A}\vc{v}_1 + \alpha_2 \mx{A}\vc{v_2} + \alpha_3 \mx{A}\vc{v_3} = \alpha_1 \lambda_1 \vc{v}_1 + \alpha_2 \lambda_2 \vc{v}_2 + \alpha_3 \lambda_3 \vc{v}_3.
\end{equation}
|
(10.109)
|
前两项仍然在该上给出一个点,而由于 $\lambda_3=0$,最后一项消失。可以将其理解为:遮挡体上的该点沿第三个的方向被投影到该上。
例 10.14:
波与振动 1
代数在理解
偏微分方程方面有许多成功应用。下面通过三个例子研究小振动。第一个例子将弦的微小振动建模为:中点有一个质量为 $m$ 的砝码。假设弦在相距为 $l$ 的两点上固定。令变量 $x$ 表示该质量相对中点的水平位移,如
例 10.8所示。
弦受到的力为 $2 T \sin(\alpha)$,其中 $\alpha$ 为图示角度。假设振幅较小,可用 $x/(l/2)$ 近似 $\sin(\alpha)$,于是力近似为
|
\begin{equation}
F = - \frac{4T}{l} x.
\end{equation}
|
(10.110)
|
由牛顿第二定律 $F = ma$ 得到微分方程
|
\begin{equation}
x'' = - \frac{4T}{ml} x .
\end{equation}
|
(10.111)
|
引入常数 $q^2 = \frac{4T}{ml}$,于是有
|
\begin{equation}
x'' = - q^2 x ,
\end{equation}
|
(10.112)
|
其解为
|
\begin{equation}
x(t) = a \sin(qt+\phi) ,
\end{equation}
|
(10.113)
|
其中 $a$ 为任意幅值,$\phi$ 为任意初相,可由初始条件确定,例如吉他弦被拨动的力度($a$)以及释放的时刻($\phi$)。
例 10.15:
波与振动 2
在本例中,我们进一步对前例进行拓展,稍微精化模型:将琴弦视为在等距位置上有三个小质量块,参见
交互插图 10.9。
与前例相同,假设弦在相距为 $l$ 的两点上固定。引入三个变量 $(x_1, x_2, x_3)$ 表示三个质量块的水平位移,如图所示。沿用小振幅近似,第一质量块的位置 $x_1$ 满足的微分方程为
|
\begin{equation}
x_1'' = - \frac{8T}{ml} x_1 + \frac{4T}{ml} x_2 .
\end{equation}
|
(10.114)
|
对另外两个距离,有
|
\begin{equation}
x_2'' = \frac{4T}{ml} x_1 - \frac{8T}{ml} x_2 + \frac{4T}{ml} x_3
\end{equation}
|
(10.115)
|
以及
|
\begin{equation}
x_3'' = \frac{4T}{ml} x_2 - \frac{8T}{ml} x_3 .
\end{equation}
|
(10.116)
|
令 $q = \frac{4T}{ml}$。这三个方程可用矩阵形式写为
|
\begin{equation}
\left(\begin{array}{c}
x_1'' \\
x_2'' \\
x_3'' \\
\end{array}\right) = q^2
\left(\begin{array}{ccc}
-2 & 1 & 0\\
1 & -2 & 1\\
0 & 1 & -2\\
\end{array}\right)
\left(\begin{array}{c}
x_1 \\
x_2 \\
x_3 \\
\end{array}\right)
\end{equation}
|
(10.117)
|
或更简洁地写为
|
\begin{equation}
\vc{x}'' = \mx{A} \vc{x} .
\end{equation}
|
(10.118)
|
该微分方程求解较为困难,主要因为三个函数 $x_1(t)$、$x_2(t)$ 与 $x_3(t)$ 相互耦合。若能将它们解耦,问题将更易处理。这正是分解能帮助我们的地方。
由于 $\mx{A}$ 是对称的,知其可由一个旋转()矩阵 $\mx{R}$ 对角化。因此有
|
\begin{equation}
\vc{x}'' = \mx{R} \mx{D}\mx{R}^\T \vc{x}
\end{equation}
|
(10.119)
|
或
|
\begin{equation}
\mx{R}^\T \vc{x}'' = \mx{D}\mx{R}^\T \vc{x} .
\end{equation}
|
(10.120)
|
通过改变坐标系,使
|
\begin{equation}
\vc{z} = \mx{R}^\T \vc{x},
\end{equation}
|
(10.121)
|
可得到解耦的方程组
|
\begin{equation}
\vc{z}'' = \mx{D} \vc{z}
\end{equation}
|
(10.122)
|
或
|
\begin{equation}
\begin{split}
z_1'' = \lambda_1 z_1, \\
z_2'' = \lambda_2 z_2,\\
z_3'' = \lambda_3 z_3. \\
\end{split}
\end{equation}
|
(10.123)
|
由于这些微分方程已解耦,可分别独立求解。
其解为
|
\begin{equation}
\begin{cases}
\begin{array}{rrrl}
z_1(t) = a_1 \sin( \sqrt{-\lambda_1} t + \phi_1), \\
z_2(t) = a_2 \sin( \sqrt{-\lambda_2} t + \phi_2), \\
z_3(t) = a_3 \sin( \sqrt{-\lambda_3} t + \phi_3).
\end{array}
\end{cases}
\end{equation}
|
(10.124)
|
最后,用 $ \vc{x} = \mx{R} \vc{z}$ 可将解表达回原坐标系
|
\begin{equation}
\begin{cases}
\begin{array}{rrrl}
x_1(t) = a_1 r_{11} \sin( \sqrt{-\lambda_1} t + \phi_1) + a_2 r_{12} \sin( \sqrt{-\lambda_2} t + \phi_2) + a_3 r_{13} \sin( \sqrt{-\lambda_3} t + \phi_3), \\
x_2(t) = a_1 r_{21} \sin( \sqrt{-\lambda_1} t + \phi_1) + a_2 r_{22} \sin( \sqrt{-\lambda_2} t + \phi_2) + a_3 r_{23} \sin( \sqrt{-\lambda_3} t + \phi_3), \\
x_3(t) = a_1 r_{31} \sin( \sqrt{-\lambda_1} t + \phi_1) + a_2 r_{32} \sin( \sqrt{-\lambda_2} t + \phi_2) + a_3 r_{33} \sin( \sqrt{-\lambda_3} t + \phi_3). \\
\end{array}
\end{cases}
\end{equation}
|
(10.125)
|
该运动由三个
特征频率刻画,它们取决于$\lambda_i$。对应每个,琴弦具有特定的空间形状,这由给出。参见
图 10.9。
要得到包含幅值($a_1$、$a_2$、$a_3$)与相位($\phi_1$、$\phi_2$、$\phi_3$)的完整解,需要初始条件的信息。在交互插图中,我们可设置 $t=0$ 时砝码的位置,从而赋值 $x_1(0)$、$x_2(0)$ 与 $x_3(0)$。这些值可直接用于
公式 (10.125),但该式较为复杂且难以求解。因此我们改用如下坐标变换:
|
\begin{equation}
\vc{z}(0) = \mx{R}^\T \vc{x}(0)
\end{equation}
|
(10.126)
|
并将新得到的约束 $\vc{z}(0)$ 代入
(10.124)中的方程。然而此时仅有三条方程却有六个未知量(全部幅值与相位),因此需要再添加三条约束。在交互插图中可通过调整初始速度 $\dot{x}_1(0)$、$\dot{x}_2(0)$ 与 $\dot{x}_3(0)$(即移动黄色箭头)来设置。对
(10.124)中的方程求导,得到
|
\begin{equation}
\begin{cases}
\begin{array}{rrrl}
\dot{z}_1(t) = a_1 \sqrt{-\lambda_1}\cos( \sqrt{-\lambda_1} t + \phi_1), \\
\dot{z}_2(t) = a_2 \sqrt{-\lambda_1}\cos( \sqrt{-\lambda_2} t + \phi_2), \\
\dot{z}_3(t) = a_3 \sqrt{-\lambda_1}\cos( \sqrt{-\lambda_3} t + \phi_3).
\end{array}
\end{cases}
\end{equation}
|
(10.127)
|
将
(10.124)中的每个方程分别除以
(10.127)中的对应方程,并令 $t=0$,得到
|
\begin{equation}
\begin{cases}
\begin{array}{rrrl}
\frac{z_1(0)}{\dot{z}_1(0)} = \frac{1}{\sqrt{-\lambda_1}}\tan( \phi_1), \\
\frac{z_2(0)}{\dot{z}_2(0)} = \frac{1}{\sqrt{-\lambda_1}}\tan( \phi_2), \\
\frac{z_3(0)}{\dot{z}_3(0)} = \frac{1}{\sqrt{-\lambda_1}}\tan( \phi_3),
\end{array}
\end{cases}
\end{equation}
|
(10.128)
|
其中 $\dot{z}(0)$ 可由 $\dot{\vc{z}}(0) = \mx{R}^\T \dot{\vc{x}}(0)$ 再次得到。由于此时有三条方程与三个未知量($\phi_1$、$\phi_2$、$\phi_3$),可求解它们,并将结果代入
(10.124)或
(10.127)中以得到 $a_1$、$a_2$、$a_3$。在交互图中,当用户移动砝码与箭头时,上述过程会自动完成。在插图的下一步中,将使用
公式 (10.125)来驱动砝码的动画。
例 10.16:
波与振动 3
在前一个例子中,我们建立了无外力作用下琴弦振动的模型。
用向量记号表示,该模型为
|
\begin{equation}
\vc{x}'' = \mx{A} \vc{x} .
\end{equation}
|
(10.129)
|
若存在外力,则它们会加到加速度项上。因此,一个合理的模型为
|
\begin{equation}
\vc{x}''(t) = \mx{A} \vc{x}(t) + \vc{u}(t).
\end{equation}
|
(10.130)
|
一个有趣的问题是:当受到正弦外力 $\vc{u}(t) = \cos(\omega t) \vc{u_0}$ 作用时,琴弦 $\vc{x}(t)$ 将如何运动。若假设存在一个特解 $\vc{x}(t) = \cos(\omega t) \vc{x}_0$,
则有
|
\begin{equation}
-\omega^2 \cos(\omega t) \vc{x}_0 = \mx{A} \cos(\omega t) \vc{x}_0 + \cos(\omega t) \vc{u}_0,
\end{equation}
|
(10.131)
|
即
|
\begin{equation}
(-\omega^2 \mx{I} - \mx{A}) \vc{x}_0 = \vc{u}_0.
\end{equation}
|
(10.132)
|
这意味着可根据输入 $\vc{u}_0$ 与频率 $\omega$ 计算振动的形状与幅度 $\vc{x}_0$,公式为
|
\begin{equation}
\vc{x}_0 = (-\omega^2 \mx{I} - \mx{A})^{-1} \vc{u}_0,
\end{equation}
|
(10.133)
|
当 $(-\omega^2 \mx{I} - \mx{A})$ 可逆时成立。若 $\det{(-\omega^2 \mx{I} - \mx{A})} = 0$,即 $-\omega^2$ 是 $\mx{A}$ 的一个时,则该矩阵不可逆。
不作细述,这些称为所谓
传递函数的
极点。
粗略地说,传递函数描述了输入 $ \vc{u}_0$ 与输出 $\vc{x}_0$ 之间的关系。
当 $-\omega^2$ 接近 $\mx{A}$ 的某个时,输出的幅度(由 $\vc{x}_0$ 的大小表征)会很大;当 $-\omega^2$ 恰等于某个时,$(-\omega^2 \mx{I} - \mx{A})$ 不可逆。此处不讨论这种情况下会发生什么。
理解系统极点的位置对于理解系统稳定性至关重要。若存在与常见噪声或扰动频率相对应的极点,可能产生不期望的后果。
1831 年 4 月 12 日,曼彻斯特附近的 Broughton 吊桥因部队整齐行进所致的输入 $u(t)$ 引发共振而坍塌。
另一著名例子是塔科马海峡大桥的坍塌,参见
此链接。
这可能并非共振,而是一种更复杂的气动弹性颤振现象。
一架从华沙飞往克拉科夫。经过一些美丽地标时,机长通过广播请所有有兴趣观景的乘客朝飞机右侧观看。许多乘客照做,结果飞机随即坠毁。为什么?
因为右侧上的极点太多。
例 10.17:
理解协方差矩阵
设有若干点 $\vc{x}_1, \ldots, \vc{x}_n$,其中每个点 $\vc{x}_i$ 用表示。其均值为向量
|
\begin{equation}
\vc{m} = \frac{1}{n} \sum_{i=1}^{n} \vc{x}_i,
\end{equation}
|
(10.134)
|
在下图中以红点表示。
协方差矩阵为
|
\begin{equation}
\mx{C} = \frac{1}{n} \sum_{i=1}^{n} (\vc{x}_i - \vc{m}) (\vc{x}_i - \vc{m})^\T .
\end{equation}
|
(10.135)
|
按定义,协方差矩阵是对称(且正定)的,因此可用矩阵 $\mx{U}$ 对角化,
|
\begin{equation}
\mx{C} = \mx{U} \mx{D} \mx{U}^\T .
\end{equation}
|
(10.136)
|
这意味着可以选择由构成的一个。
$\mx{U} = \begin{pmatrix} \vc{u}_1 & \ldots & \vc{u}_n \end{pmatrix}$ 的列即为这些。假设按照对应的 $\lambda_1, \ldots, \lambda_n$ 的降序排列,即 $\lambda_1 \geq \ldots \geq \lambda_n \geq 0$。这意味着
$\vc{u}_1$ 对应方差最大的方向,$\sqrt{\lambda_1}$ 对应该方向上的标准差。图中,$\sqrt{\lambda_1}$ 乘以 $\vc{u}_1$ 为两根箭头中较长的那一根,
$\sqrt{\lambda_2}$ 乘以 $\vc{u}_2$ 为较短的一根。
参见
交互插图 10.10。
例 10.18:
特征人脸
其核心思想是可以通过
学习掌握人脸图像的分布特征,并据此用于
图像/
视频压缩、
人脸检测或
人脸识别等任务。简而言之,先对一组图像计算均值与协方差矩阵,然后计算该协方差矩阵的
与
。对应最大的最能表征图像中的变化。
这是一个
机器学习的例子。更一般地说,
机器学习是用于学习数据的良好表示,或学习如何识别图像的工具。相关方法通常涉及代数、数理统计、分析与优化,并应用于(通常很大的)数据集合。
在本例中,我们收集了若干人脸图像,见
图 10.11。
图像可以看作向量空间中的元素。
每幅图像 $\vc{W}$ 由 $m$ 行、$n$ 列的像素强度构成,即
|
\begin{equation}
\vc{W} =
\begin{pmatrix}
w_{1,1} & w_{1,2} & \ldots & w_{1,n} \\
w_{2,1} & w_{2,2} & \ldots & w_{2,n} \\
\vdots & \vdots & \vdots & \vdots \\
w_{m,1} & w_{m,2} & \ldots & w_{m,n}
\end{pmatrix}.
\end{equation}
|
(10.137)
|
然而,此处我们把 $\vc{W}$ 视为向量空间的元素,而不再把 $\vc{W}$ 看作可与向量相乘的矩阵!
按列堆叠的方式,引入从图像到的,即
|
\begin{equation}
\begin{pmatrix}
x_{1} \\
x_{2} \\
\vdots \\
x_{m} \\
x_{m+1} \\
x_{m+2} \\
\vdots \\
x_{m+m} \\
\vdots \\
x_{m(n-1)+1} \\
x_{m(n-1)+2} \\
\vdots \\
x_{N}
\end{pmatrix}
= \vc{x} = f(\vc{W})
= \begin{pmatrix}
w_{1,1} \\
w_{2,1} \\
\vdots \\
w_{m,1} \\
w_{1,2} \\
w_{2,2} \\
\vdots \\
w_{m,2} \\
\vdots \\
w_{1,n} \\
w_{2,n} \\
\vdots \\
w_{m,n}
\end{pmatrix} ,
\end{equation}
|
(10.138)
|
其中 $N = mn$。同时引入从 $\vc{x}$ 到图像 $\vc{W}$ 的逆,即
|
\begin{equation}
\begin{pmatrix}
w_{1,1} & w_{1,2} & \ldots & w_{1,n} \\
w_{2,1} & w_{2,2} & \ldots & w_{2,n} \\
\vdots & \vdots & \vdots & \vdots \\
w_{m,1} & w_{m,2} & \ldots & w_{m,n}
\end{pmatrix}
= \vc{w} = f^{-1}(\vc{x})
=
\begin{pmatrix}
x_{1} & x_{m+1} & \ldots & x_{m (n-1) + 1} \\
x_{2} & x_{m+2} & \ldots & x_{m (n-1) + 2} \\
\vdots & \vdots & \vdots & \vdots \\
x_{m} & x_{m+m} & \ldots & x_{m n}
\end{pmatrix} .
\end{equation}
|
(10.139)
|
换言之,$f$ 接受一幅图像并产生一个很长的,而 $f^{-1}$ 接受一个并生成一幅图像。
假设我们有一组图像 $\vc{W}_1, \ldots, \vc{W}_{23}$,如
图 10.11所示。
这些图像尺寸均为 $81 \times 41$ 像素。通过 $\vc{x}_i = f(\vc{W}_i)$ 将每幅图像到对应的,得到 $23$ 个向量 $\vc{x}_1, \ldots, \vc{x}_{23}$,其中每个向量的大小为
$3321 \times 1$。其均值为向量
|
\begin{equation}
\vc{m} = \frac{1}{n} \sum_{i=1}^{n} \vc{x}_i ,
\end{equation}
|
(10.140)
|
将其从向量转换回图像即可可视化该均值,即 $\vc{O} = f^{-1}(\vc{m)}$。
协方差矩阵为
|
\begin{equation}
\mx{C} = \frac{1}{n} \sum_{i=1}^{n} (\vc{x}_i - \vc{m}) (\vc{x}_i - \vc{m})^\T .
\end{equation}
|
(10.141)
|
与前一例相同,我们用矩阵 $\mx{U}$ 分解协方差矩阵,
|
\begin{equation}
\mx{C} = \mx{U} \mx{D} \mx{U}^\T,
\end{equation}
|
(10.142)
|
我们再次按对应的对进行排序,即将 $\mx{U} = \begin{pmatrix} \vc{u}_1 & \ldots & \vc{u}_N \end{pmatrix}$ 的各列按 $\lambda_1, \ldots, \lambda_N$ 的降序排列($\lambda_1 \geq \ldots \geq \lambda_N \geq 0$)。这意味着
$\vc{u}_1$ 对应变化最大的方向,$\sqrt{\lambda_1}$ 为该方向上的标准差。
在本例中,我们选择对应于最大两个的两个向量作为特征人脸(将向量转换为图像后,$\vc{E}_1 = f^{-1}(\sqrt{\lambda_1} \vc{u}_1)$ 与
$\vc{E}_2 = f^{-1}(\sqrt{\lambda_2} \vc{u}_2)$)。
下图从左到右依次显示这三幅图像 $\vc{O}$、$\vc{E}_1$ 与 $\vc{E}_2$。
本章最后给出一个例子,以说明该主题还有更多内容可供深入学习。
例 10.19:
关于与的理论远不止方阵这一情形。
本节略作旁引,旨在展示本章某些概念的普适性。
我们可以研究一般或算子的。一个有趣的例子是对函数求导这一操作。它是的,但导数算子是否存在“”(或特征函数)?
将“求导”视为一个算子 $D$:输入函数 $g$,输出函数 $h$。
|
\begin{equation}
h = D(g) = \frac{d}{dx} g .
\end{equation}
|
(10.143)
|
考察如下指数函数 $g$:
|
\begin{equation}
g(x) = e^{\lambda x} .
\end{equation}
|
(10.144)
|
对 $g$ 求导得到:
|
\begin{equation}
D(g) = \frac{d}{dx} g = \lambda e^{\lambda x} = \lambda g
\end{equation}
|
(10.145)
|
因此有 $D(g) = \lambda g$。也就是说,$g$ 是导数算子的“”,其“”为 $\lambda$。
不过这已稍微偏离本课程的核心主题。
弹出帮助:
$n$ 维列向量 $\vc{v}$ 相对于某个来表示,由 $n$ 个标量值组成一列。
其分量有时记为 $v_1, v_2, \ldots, v_n$。对二维与三维向量,也常用 $v_x, v_y, v_z$ 记号。
记法如下:
|
\begin{equation}
\underbrace{
\vc{u} =
\begin{pmatrix}
u_x
\end{pmatrix}
=
\begin{pmatrix}
u_1
\end{pmatrix}}_{\text{1D vector}},
\spc\spc
\underbrace{
\vc{v} =
\begin{pmatrix}
v_x \\
v_y
\end{pmatrix}
=
\begin{pmatrix}
v_1 \\
v_2
\end{pmatrix}}_{\text{2D vector}},
\spc\spc
\underbrace{
\vc{w} =
\begin{pmatrix}
w_x \\
w_y \\
w_z
\end{pmatrix}
=
\begin{pmatrix}
w_1 \\
w_2 \\
w_3
\end{pmatrix}}_{\text{3D vector}},
\end{equation}
|
|
其中 $\vc{u} = u_x \vc{e}_1$,$\vc{v} = v_x \vc{e}_1 + v_y \vc{e}_2$,
以及 $\vc{w} = w_x \vc{e}_1 + w_y \vc{e}_2 + w_z \vc{e}_3$。
注意 $\vc{e}_i$ 是向量。
本文也使用简写 $\vc{w} = \bigl(w_1,w_2,w_3\bigr)$,其含义与上式相同(注意分量之间的逗号)。
而行向量通常不使用逗号分隔。


 用于生成 $\vc{O}$、$\vc{E}_1$ 和 $\vc{E}_2$ 的图像见图 10.2。在学习更多特征值与特征向量之后,我们会在例 10.18对该过程做更详细解释。简要来说,图 10.2中的图像用于计算均值 $O$ 和协方差矩阵。协方差矩阵对应最大两个特征值的特征向量被用作 $\vc{E}_1$ 与 $\vc{E}_2$。
用于生成 $\vc{O}$、$\vc{E}_1$ 和 $\vc{E}_2$ 的图像见图 10.2。在学习更多特征值与特征向量之后,我们会在例 10.18对该过程做更详细解释。简要来说,图 10.2中的图像用于计算均值 $O$ 和协方差矩阵。协方差矩阵对应最大两个特征值的特征向量被用作 $\vc{E}_1$ 与 $\vc{E}_2$。



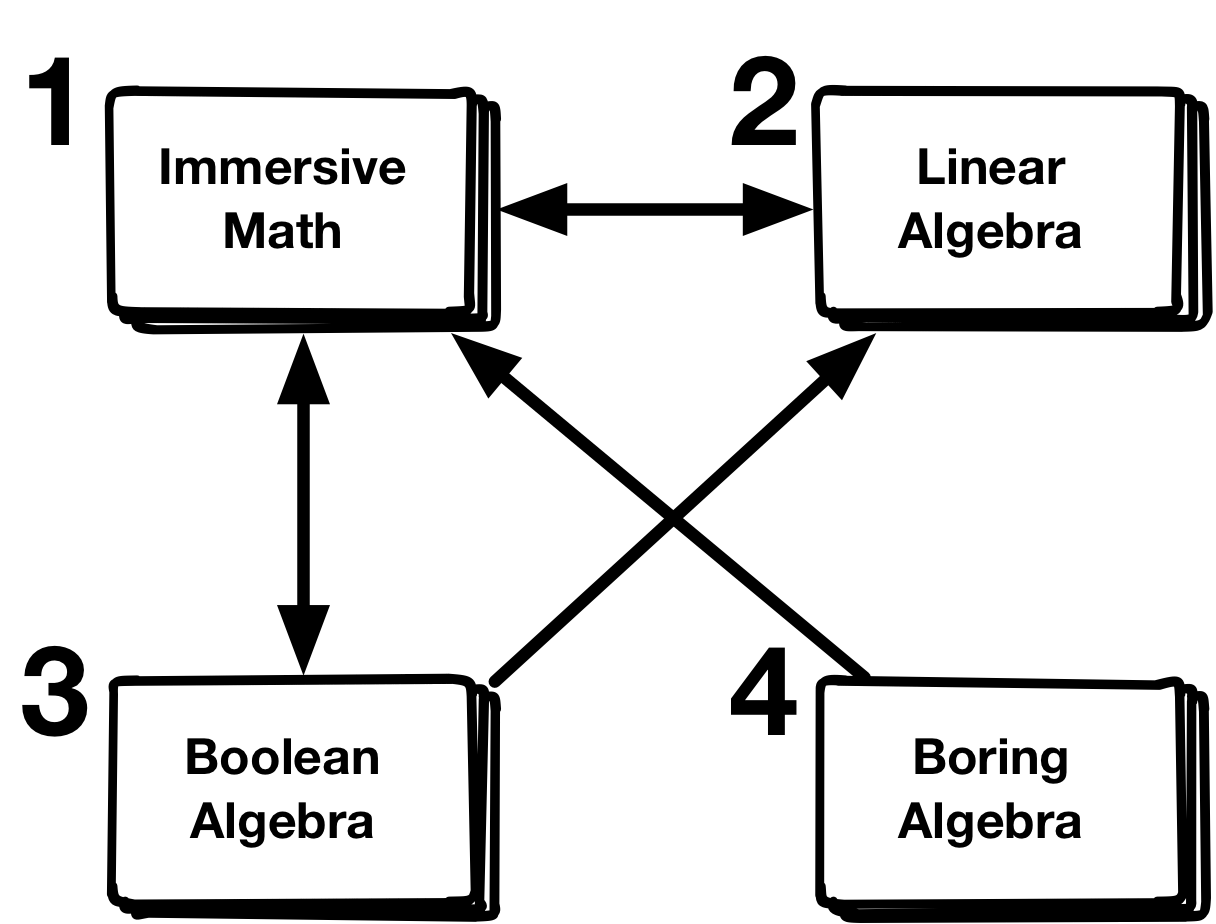 从一个主页到另一个主页的链接在图中用箭头表示。
设处在各主页上的概率由向量 $\vc{v} = \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \end{pmatrix}$ 给出,其中 $v_i$ 是处在编号为 $i$ 的主页上的概率。如果在某个主页上随机选择其链接,则处在各主页上的概率变为 $ \vc{w} = \mx{A} \vc{v}$,
其中转移矩阵 $\mx{A}$ 为:
从一个主页到另一个主页的链接在图中用箭头表示。
设处在各主页上的概率由向量 $\vc{v} = \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \end{pmatrix}$ 给出,其中 $v_i$ 是处在编号为 $i$ 的主页上的概率。如果在某个主页上随机选择其链接,则处在各主页上的概率变为 $ \vc{w} = \mx{A} \vc{v}$,
其中转移矩阵 $\mx{A}$ 为:








